题目内容
12.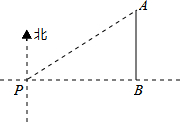 如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置B,海轮航行的距离AB为1海里.
如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置B,海轮航行的距离AB为1海里.
分析 首先由方向角的定义及已知条件得出∠NPA=60°,AP=2海里,∠ABP=90°,再由AB∥NP,根据平行线的性质得出∠A=∠NPA=60°.然后解Rt△ABP,得出AB=AP•cos∠A=1海里.
解答 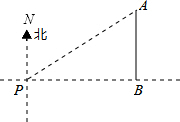 解:如图,由题意可知∠NPA=60°,AP=2海里,∠ABP=90°.
解:如图,由题意可知∠NPA=60°,AP=2海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=60°.
在Rt△ABP中,∵∠ABP=90°,∠A=60°,AP=2海里,
∴AB=AP•cos∠A=2×cos60°=2×$\frac{1}{2}$=1海里.
故答案为1.
点评 本题考查了解直角三角形的应用-方向角问题,平行线的性质,三角函数的定义,正确理解方向角的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.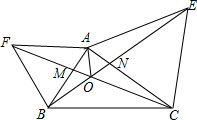 如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠AMO=∠ANO;③OA平分∠FOE;④∠COB=120°,其中正确的有( )
如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠AMO=∠ANO;③OA平分∠FOE;④∠COB=120°,其中正确的有( )
 如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠AMO=∠ANO;③OA平分∠FOE;④∠COB=120°,其中正确的有( )
如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠AMO=∠ANO;③OA平分∠FOE;④∠COB=120°,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.|1-tan45°|的值为( )
| A. | $\frac{1}{2}$ | B. | 1-$\frac{{\sqrt{2}}}{2}$ | C. | 1-$\frac{{\sqrt{3}}}{2}$ | D. | 0 |
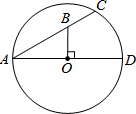 如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD交AC于点B.若OB=4,则BC长为( )
如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD交AC于点B.若OB=4,则BC长为( )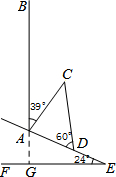 如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.
如图,山坡上有一颗大树AB与水平面EF垂直,海啸过后,大树被刮倾斜后折断倒在山坡上,树的顶部D恰好接触到坡面AE.已知山坡的坡角∠AEF=24°,测得树干的倾斜角∠BAC=39°,大树被折断部分CD和坡面的夹角∠ADC=60°,AD=4米.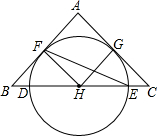 如图,在△ABC中,AB=AC,BC经过⊙H的圆心交⊙H于点D、E,AB、AC是圆的切线,F、G是切点.
如图,在△ABC中,AB=AC,BC经过⊙H的圆心交⊙H于点D、E,AB、AC是圆的切线,F、G是切点.