题目内容
15．
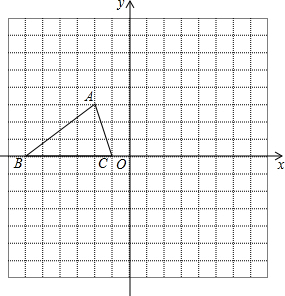△ABC在平面直角坐标系中的位置如图所示，A、B、C三点在格点上：（1）画出△ABC关于x轴对称的图形△A1B1C1
（2）若点M（a，b）是△ABC内任意一点，则△A1B1C1中与点M对应的点M1的坐标为（a，-b）．
分析 （1）根据关于x轴对称的点的坐标特征写出A、B、C的对称点A1、B1、C1的坐标，然后描点即可得到△A1B1C1；
（2）根据关于x轴对称的点的坐标特征求解．
解答 解：（1）如图，△A1B1C1为所作；
（2）△A1B1C1中与点M对应的点M1的坐标为（a，-b）．
故答案为（a，-b）．
点评 本题考查了作图-轴对称变换：几何图形都可看做是有点组成，我们在画一个图形的轴对称图形时，也是先从确定一些特殊的对称点开始的，一般的方法是：由已知点出发向所给直线作垂线，并确定垂足；直线的另一侧，以垂足为一端点，作一条线段使之等于已知点和垂足之间的线段的长，得到线段的另一端点，即为对称点；连接这些对称点，就得到原图形的轴对称图形．
练习册系列答案
相关题目
5．已知a，b，c为△ABC三边，且满足（a2-b2）（a2+b2-c2）=0，则它的形状为（ ）
| A． | 直角三角形 | B． | 等腰三角形 | ||
| C． | 等腰直角三角形 | D． | 等腰三角形或直角三角形 |
3．
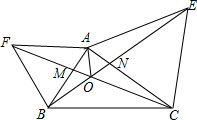如图，已知AF=AB，∠FAB=60°，AE=AC，∠EAC=60°，CF和BE交于O点，则下列结论：①CF=BE；②∠AMO=∠ANO；③OA平分∠FOE；④∠COB=120°，其中正确的有（ ）
如图，已知AF=AB，∠FAB=60°，AE=AC，∠EAC=60°，CF和BE交于O点，则下列结论：①CF=BE；②∠AMO=∠ANO；③OA平分∠FOE；④∠COB=120°，其中正确的有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
20．|1-tan45°|的值为（ ）
| A． | $\frac{1}{2}$ | B． | 1-$\frac{{\sqrt{2}}}{2}$ | C． | 1-$\frac{{\sqrt{3}}}{2}$ | D． | 0 |
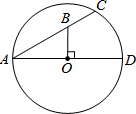如图，AD，AC分别是⊙O的直径和弦．且∠CAD=30°．OB⊥AD交AC于点B．若OB=4，则BC长为（ ）
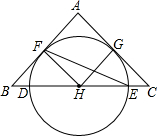如图，在△ABC中，AB=AC，BC经过⊙H的圆心交⊙H于点D、E，AB、AC是圆的切线，F、G是切点．