题目内容
17.若1≤x≤2,求y=2x2-x+1的最大值、最小值.分析 求出顶点坐标,再求出x=1,x=2时的y的值,然后作出判断.
解答 解:当x=1时,y=2,
当x=2时,y=7,
又∵y=2x2-x+1=2(x-$\frac{1}{4}$)2+$\frac{7}{8}$.
∴x=$\frac{1}{4}$时,y最小值=$\frac{7}{8}$,
综上所述若1≤x≤2时,y=2x2-x+1的最大值是7、最小值是2.
点评 本题考查二次函数的最值问题,需要熟练掌握配方法求顶点坐标,会判断最值问题,注意自变量x在端点时函数值y的取值,属于中考常考题型.

练习册系列答案
相关题目
9.已知关于x的方程(a+5b)x-5=0无解,那么方程ax-b=0解的情况( )
| A. | 有一解 | B. | 有无数解 | C. | 有一解或无数解 | D. | 无解 |
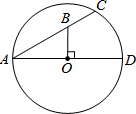 如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD交AC于点B.若OB=4,则BC长为( )
如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD交AC于点B.若OB=4,则BC长为( )