题目内容
12.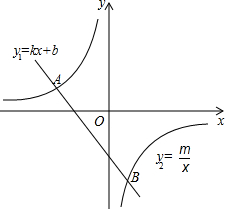 如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-3,1)、B(1.5,n)两点.若y1>y2,则x的取值范围是x<-3或0<x<1.5.
如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-3,1)、B(1.5,n)两点.若y1>y2,则x的取值范围是x<-3或0<x<1.5.
分析 把(-3,1)代入数y2=$\frac{m}{x}$得m=-3,则B的坐标即可求得,然后根据求y1>y2时x的取值范围,就是求一次函数的图象在反比例函数的上边时对应的x的范围.
解答 解:把(-3,1)代入数y2=$\frac{m}{x}$得m=-3,
则反比例函数的解析式是y=-$\frac{3}{x}$.
在y=-$\frac{3}{x}$中令x=1.5,解得y=n=-2.
则B的坐标是(1.5,-2).
根据图象可得若y1>y2,则x的取值范围是:x<-3或0<x<1.5.
故答案是:x<-3或0<x<1.5.
点评 本题考查了用待定系数法求出一次函数、反比例函数的解析式,一次函数与反比例函数的交点问题的应用,主要考查学生能否运用这些性质进行计算,本题具有一定的代表性,是一道不错的题目,数形结合思想的运用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
4.一个寻宝游戏的通道平面图如图1所示(正方形ABCD是⊙O的内接四边形),图中的所有线段和弧线都是通道.为了记录寻宝者的行进路线,相关人员在点O处放置了一台定位仪器.设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x之间的函数关系的图象如图2所示,则寻宝者的行进路线可能为…( )
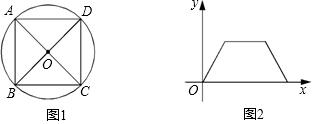

| A. | 线段OA→劣弧AD→线段DO | B. | 劣弧AD→线段DO→线段OC | ||
| C. | 劣弧AD→劣弧DC→线段CO | D. | 线段OB→劣弧BC→劣弧CD |
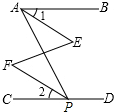 如图,∠BAP+∠APD=180°,∠1=∠2,∠E=40°,试求∠F的度数.
如图,∠BAP+∠APD=180°,∠1=∠2,∠E=40°,试求∠F的度数. 已知反比例函数y=$\frac{k}{x}$的图象经过点(-3,4).
已知反比例函数y=$\frac{k}{x}$的图象经过点(-3,4).