题目内容
13.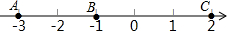 如图,数轴上的点A、B、C分别表示数-3、-1、2.
如图,数轴上的点A、B、C分别表示数-3、-1、2.(1)A、B两点的距离AB=2,A、C两点的距离AC=5;
(2)通过观察,可以发现数轴上两点间距离与这两点表示的数的差的绝对值有一定关系,按照此关系,若点E表示的数为x,则AE=|x+3|;
(3)利用数轴直接写出|x-1|+|x+3|的最小值=4.
分析 (1)直接利用数轴可得AB,AC的长;
(2)结合数轴可得出点E表示的数为x,则AE的长为:|x+3|;
(3)直接利用数轴可得出|x-1|+|x+3|的最小值.
解答 解:(1)如图所示:AB=2,AC=5.
故答案为:2,5;
(2)根据题意可得:AE=|x+3|.
故答案为:|x+3|;
(3)利用数轴可得:|x-1|+|x+3|的最小值为:4.
故答案为:4.
点评 此题主要考查了绝对值以及数轴的应用,正确结合数轴表示线段长度是解题关键.

练习册系列答案
相关题目
1.代数式2x+3与5互为相反数,则x等于( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
8.某商场计划购进甲,乙两种空气净化机共500台,这两种空气净化机的进价、售价如下表:
解答下列问题:
(1)按售价售出一台甲种空气净化机的利润是500元.
(2)若两种空气净化机都能按售价卖出,问如何进货能使利润恰好为450 000元?
| 进价(元/台) | 售价(元/台) | |
| 甲种空气净化机 | 3000 | 3500 |
| 乙种空气净化机 | 8500 | 10000 |
(1)按售价售出一台甲种空气净化机的利润是500元.
(2)若两种空气净化机都能按售价卖出,问如何进货能使利润恰好为450 000元?
18.分式$-\frac{1}{1-x}$可变形为( )
| A. | $\frac{1}{x+1}$ | B. | $-\frac{1}{x+1}$ | C. | $-\frac{1}{x-1}$ | D. | $\frac{1}{x-1}$ |
 用8个相同的小正方体搭成一个几何体,从上面看它得到的平面图形如图所示,那么从左面看它得到的平面图形一定不是( )
用8个相同的小正方体搭成一个几何体,从上面看它得到的平面图形如图所示,那么从左面看它得到的平面图形一定不是( )



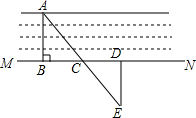 如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是:ASA,全等三角形对应边相等.
如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是:ASA,全等三角形对应边相等.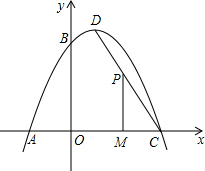 如图,一抛物线经过点A(-2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.
如图,一抛物线经过点A(-2,0),点B(0,4)和点C(4,0),该抛物线的顶点为D.