题目内容
16.先化简,再求值:${a^3}•{(-\frac{1}{2}{b^3})^2}+{(-\frac{1}{2}a{b^2})^3}$,其中a=-2,b=1.分析 先算乘方,再算乘法,合并同类项,最后代入求出即可.
解答 解:${a^3}•{(-\frac{1}{2}{b^3})^2}+{(-\frac{1}{2}a{b^2})^3}$
=a3•$\frac{1}{4}$b6+(-$\frac{1}{8}$a3b6)
=$\frac{1}{4}$a3b6+(-$\frac{1}{8}$a3b6)
=$\frac{1}{8}{a^3}{b^6}$,
当a=-2,b=1时,原式=$\frac{1}{8}$×(-2)3×16=-1.
点评 本题考查了整式的混合运算和求值的应用,能正确运用整式的运算法则进行化简是解此题的关键.

练习册系列答案
相关题目
11.已知∠A=35°10′48″,则∠A的余角是( )
| A. | 144.82° | B. | 54.82° | C. | 54.42° | D. | 144.42° |
1.代数式2x+3与5互为相反数,则x等于( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
8.某商场计划购进甲,乙两种空气净化机共500台,这两种空气净化机的进价、售价如下表:
解答下列问题:
(1)按售价售出一台甲种空气净化机的利润是500元.
(2)若两种空气净化机都能按售价卖出,问如何进货能使利润恰好为450 000元?
| 进价(元/台) | 售价(元/台) | |
| 甲种空气净化机 | 3000 | 3500 |
| 乙种空气净化机 | 8500 | 10000 |
(1)按售价售出一台甲种空气净化机的利润是500元.
(2)若两种空气净化机都能按售价卖出,问如何进货能使利润恰好为450 000元?

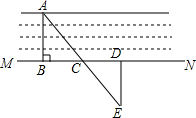 如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是:ASA,全等三角形对应边相等.
如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是:ASA,全等三角形对应边相等.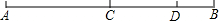 如图,点C,D在线段AB上,CD=4cm,AB=12cm,则图中所有线段的和是多少?
如图,点C,D在线段AB上,CD=4cm,AB=12cm,则图中所有线段的和是多少?