题目内容
1.如果方程2-$\frac{x+1}{3}=\frac{x+7}{6}$的解也是方程2-$\frac{a-x}{3}=0$的解,那么a的值是( )| A. | 7 | B. | 5 | C. | 3 | D. | 以上都不对 |
分析 先求得方程2-$\frac{x+1}{3}=\frac{x+7}{6}$的解,然后将方程的解代入2-$\frac{a-x}{3}=0$解得a的值即可.
解答 解:2-$\frac{x+1}{3}=\frac{x+7}{6}$
去分母得:12-2(x+1)=x+7,
去括号的:12-2x-2=x+7,
移项得:-2x-x=7-12+2,
合并同类项得:-3x=-3,
系数化为1得:x=1.
将x=1代入2-$\frac{a-x}{3}=0$得:2-$\frac{a-1}{3}$=0,
去分母得:6-(a-1)=0
去括号得:6-a+1=0
解得:a=7.
故选:A
点评 本题主要考查的是同解方程的定义、一元一次方程的解法,掌握相关知识是解题的关键.

练习册系列答案
相关题目
11.用四舍五入法把3.1415926…精确到0.001得到的近似值是( )
| A. | 3.14 | B. | 3.142 | C. | 3.1416 | D. | 3.146 |
16.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,…,依此类推,则a2015的值为( )
| A. | -1005 | B. | -1006 | C. | -1007 | D. | -2014 |
6.已知a,b,c是△ABC的三边长,且满足|a-b|+$\sqrt{c-b}$=0,则是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 不能确定 |
 解不等式组$\left\{\begin{array}{l}{x-3(x-2)≤8}\\{5-\frac{1}{2}x>2x}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{x-3(x-2)≤8}\\{5-\frac{1}{2}x>2x}\end{array}\right.$,并把解集在数轴上表示出来. 如图,△ABC中,AB=41,BC=15,CA=52,AM平分∠BAC,点D、E分别为AM、AB上的动点,则BD+DE的最小值是9.
如图,△ABC中,AB=41,BC=15,CA=52,AM平分∠BAC,点D、E分别为AM、AB上的动点,则BD+DE的最小值是9. 如图,△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE分别交AC、AB于点D、E.求∠CBD的度数.
如图,△ABC中,AB=AC,∠A=50°,AB的垂直平分线DE分别交AC、AB于点D、E.求∠CBD的度数.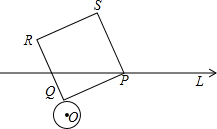 ⊙O是半径为1的圆,点O到直线L的距离为3,过直线L上的任一点P作⊙O的切线,切点为Q;若以PQ为边作正方形PQRS,则正方形PQRS的面积最小为( )
⊙O是半径为1的圆,点O到直线L的距离为3,过直线L上的任一点P作⊙O的切线,切点为Q;若以PQ为边作正方形PQRS,则正方形PQRS的面积最小为( )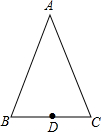 如图,等腰三角形ABC的底边BC的长为6cm,面积是27cm2,D为BC边长的中点.
如图,等腰三角形ABC的底边BC的长为6cm,面积是27cm2,D为BC边长的中点.