题目内容
9.如图,菱形ABCD中,AB=2,∠C=60°,我们把菱形ABCD的对称中心O称作菱形的中心,菱形ABCD在直线L上向右作无滑动的翻滚,每绕着一个顶点旋转60°叫做一次操作,则经过2013次这样的操作菱形中心O所经过的路径总长为( )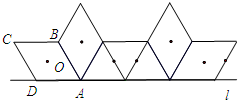
| A. | $\frac{{671(\sqrt{3}+1)}}{3}$π | B. | $\frac{{671(2\sqrt{3}+1)}}{2}$π | C. | $\frac{{671(2\sqrt{3}+1)}}{3}$π | D. | $\frac{{1342\sqrt{3}}}{3}$π |
分析 从图中可以看出,第一次旋转是以点A为圆心,那么菱形中心旋转的半径就是OA,解直角三角形可求出OA的长,圆心角是60°.第二次还是以点A为圆心,那么菱形中心旋转的半径就是OA,圆心角是60°.第三次就是以点B为旋转中心,OB为半径,旋转的圆心角为60度.旋转到此菱形就又回到了原图.故这样旋转3n次,就是这样的n个弧长的总长,依此计算即可得,进而得出经过2013(n为正整数)次这样的操作菱形中心O所经过的路径总长.
解答 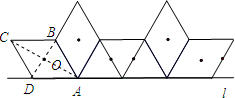 解:∵菱形ABCD中,AB=2,∠C=60°,
解:∵菱形ABCD中,AB=2,∠C=60°,
∴△ABD是等边三角形,
BO=DO=1,
AO=$\sqrt{{AD}^{2}-{DO}^{2}}$=$\sqrt{3}$,
第一次旋转的弧长=$\frac{60π×\sqrt{3}}{180}$=$\frac{\sqrt{3}}{3}$π,
∵第一、二次旋转的弧长和=$\frac{60π×\sqrt{3}}{180}$+$\frac{60π×\sqrt{3}}{180}$=$\frac{2\sqrt{3}}{3}$π,
第三次旋转的弧长为:$\frac{60π×1}{180}$=$\frac{π}{3}$,
∵3n÷3=n,
∴经过3n(n为正整数)次这样的操作菱形中心O所经过的路径总长为:n×($\frac{2\sqrt{3}}{3}$π+$\frac{π}{3}$)=$\frac{2\sqrt{3}+1}{3}$nπ.
∵2013÷3=671,
∴经过2013次这样的操作菱形中心O所经过的路径总长=$\frac{671(2\sqrt{3}+1)}{3}$π.
故选C.
点评 本题主要考查了弧长的计算公式以及菱形的性质,根据已知得出菱形每转动3次一循环进而得出经过路径是解题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
6.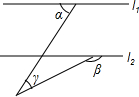 如图,l1∥l2,则下列式子成立的是( )
如图,l1∥l2,则下列式子成立的是( )
 如图,l1∥l2,则下列式子成立的是( )
如图,l1∥l2,则下列式子成立的是( )| A. | ∠α+∠β+∠γ=180° | B. | ∠α+∠β-∠γ=180° | C. | ∠β+∠γ-∠α=180° | D. | ∠α-∠β+∠γ=180° |
14.一批货物要运往某地,货主准备租用甲、乙两种货车,过去两次租用这种货车的情况如下表:
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,问:这批货共有多少吨?
| 第一次 | 第二次 | |
| 甲种货车辆数(辆) | 2 | 5 |
| 乙种货车辆数(辆) | 3 | 6 |
| 累计运货吨数(吨) | 15.5 | 35 |
 已知:如图,∠BCA=∠DAC.求证:∠B与∠DAB互补.
已知:如图,∠BCA=∠DAC.求证:∠B与∠DAB互补. 抛物线y=x2-x-6与x轴交于点A、B(A在B的左边),与y轴分别交于点C.
抛物线y=x2-x-6与x轴交于点A、B(A在B的左边),与y轴分别交于点C.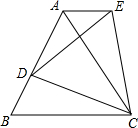 如图,△ABC是边长为2的等边三角形,D是AB边上的一点,把线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
如图,△ABC是边长为2的等边三角形,D是AB边上的一点,把线段CD绕点C顺时针旋转60°得到线段CE,连接AE.