题目内容
15.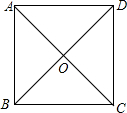 如图是一个边长为a的正方形.两条对角线AC与BD相交于O.观察此图并回答下面问题:
如图是一个边长为a的正方形.两条对角线AC与BD相交于O.观察此图并回答下面问题:(1)对角线AC有多长呢?
(2)图中有多少个直角三角形?
分析 (1)由正方形的性质和勾股定理,即可得出AC的长;
(2)由正方形的性质即可得出直角三角形的个数.
解答 解:(1)∵四边形ABCD是正方形,
∴AB=BC=CD=AD=a,∠ABC=∠BCD=∠CDA=∠BAD=90°,AC=BD,AC⊥BD,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{a}^{2}+{a}^{2}}$=$\sqrt{2}$a;
(2)∵∠ABC=∠BCD=∠CDA=∠BAD=90°,AC⊥BD,
∴直角三角形有△ABC、△BCD、△CDA、△DAB,△AOB、△BOC、△COD、△AOD共8个.
点评 本题考查了正方形的性质、勾股定理;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
20.下列叙述正确的是( )
| A. | 所有的直角三角形都相似 | B. | 所有的等腰三角形都相似 | ||
| C. | 所有的等腰直角三角形都相似 | D. | 所有的矩形都相似 |
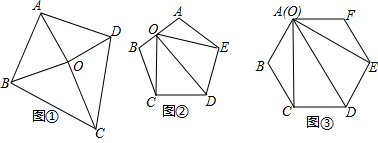
 如图,求∠A+∠B+∠C+∠D+∠E-∠F-∠G的度数.
如图,求∠A+∠B+∠C+∠D+∠E-∠F-∠G的度数.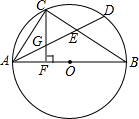 如图,AB是⊙O的直径,D是$\widehat{AB}$上一点,C是弧$\widehat{AD}$的中点,AD、BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:CG=EG.
如图,AB是⊙O的直径,D是$\widehat{AB}$上一点,C是弧$\widehat{AD}$的中点,AD、BC相交于E,CF⊥AB,F为垂足,CF交AD于G,求证:CG=EG. 已知:如图,∠BCA=∠DAC.求证:∠B与∠DAB互补.
已知:如图,∠BCA=∠DAC.求证:∠B与∠DAB互补.