题目内容
 直线AB、CD相交于点O,OE平分∠AOC,∠FOD=90°,∠2:∠3=8:11,求∠1和∠EOF的度数.
直线AB、CD相交于点O,OE平分∠AOC,∠FOD=90°,∠2:∠3=8:11,求∠1和∠EOF的度数.考点:对顶角、邻补角,角平分线的定义
专题:
分析:由OE平分∠AOC,可得:∠3=∠4,由∠2:∠3=8:11,可得:∠2:∠3:∠4=8:11:11,然后根据平角的定义,可求∠2、∠3、∠4的度数,由∠FOD=90°,根据平角的定义,可得∠1+∠2=90°,进而求出∠1的度数,然后由对顶角相等,可求∠5的度数,进而可求∠EOF的度数.
解答:解:∵OE平分∠AOC,
∴∠3=∠4,
∵∠2:∠3=8:11,
∴∠2:∠3:∠4=8:11:11,
设∠2=8x,∠3=11x,∠4=11x,
∵∠2+∠3+∠4=180°,
∴8x+11x+11x=180°,
解得:x=6°,
∵∠2=48°,∠3=66°,∠4=66°,
∵∠5与∠2是对顶角,
∴∠5=∠2=48°,
∵∠FOD=90°,∠1+∠2+∠FOD=180°,
∴∠1+∠2=90°,
∴∠1=42°,
∵∠EOF=∠1+∠4+∠5,
∴∠EOF=42°+66°+48°=156°,
∴∠1=42°,∠EOF=156°.
∴∠3=∠4,
∵∠2:∠3=8:11,
∴∠2:∠3:∠4=8:11:11,
设∠2=8x,∠3=11x,∠4=11x,
∵∠2+∠3+∠4=180°,
∴8x+11x+11x=180°,
解得:x=6°,
∵∠2=48°,∠3=66°,∠4=66°,
∵∠5与∠2是对顶角,
∴∠5=∠2=48°,
∵∠FOD=90°,∠1+∠2+∠FOD=180°,
∴∠1+∠2=90°,
∴∠1=42°,
∵∠EOF=∠1+∠4+∠5,
∴∠EOF=42°+66°+48°=156°,
∴∠1=42°,∠EOF=156°.
点评:此题考查了平角的定义、对顶角的性质及角平分线的性质,解题的关键是先求出∠2的度数.

练习册系列答案
相关题目
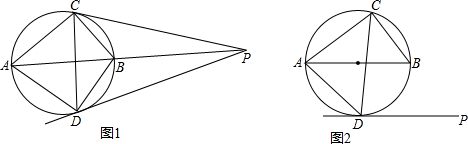
 如图,A,B是小河同侧的两个村庄,为解决吃水问题,两村合资在河边修一个水站.
如图,A,B是小河同侧的两个村庄,为解决吃水问题,两村合资在河边修一个水站.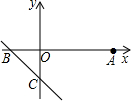 如图,已知A(2,0)、B(-1,0)、C(0,-1),在直线BC上是否存在一点P,使△ACP为等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
如图,已知A(2,0)、B(-1,0)、C(0,-1),在直线BC上是否存在一点P,使△ACP为等腰三角形?若存在,求点P的坐标;若不存在,说明理由. 如图,直线y=x-3与反比例函数y=
如图,直线y=x-3与反比例函数y=