题目内容
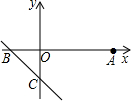 如图,已知A(2,0)、B(-1,0)、C(0,-1),在直线BC上是否存在一点P,使△ACP为等腰三角形?若存在,求点P的坐标;若不存在,说明理由.
如图,已知A(2,0)、B(-1,0)、C(0,-1),在直线BC上是否存在一点P,使△ACP为等腰三角形?若存在,求点P的坐标;若不存在,说明理由.考点:等腰三角形的判定,坐标与图形性质
专题:
分析:设出点P的横坐标,根据直线BC的解析式表示出P点的纵坐标,然后利用坐标系两点间的距离公式分别表示出△ACP三边的长,从而根据:①AP=CP、②AC=AP、③CP=AC,三种不同等量关系求出符合条件的P点坐标.
解答:解:设直线BC的解析式为y=kx+b,
代入点B(-1,0)、C(0,-1),
求得y=-x-1;
设P(x,-x-1),因为A(2,0),C(0,-1),则有:
AP2=(x-2)2+(-x-1)2=2x2-2x+5,
AC2=5,CP2=x2+(-x-1+1)2=2x2;
①当AP=CP时,AP2=CP2,有:
2x2-2x+5=2x2,解得x=2.5,
∴P1(2.5,-3.5);
②当AP=AC时,AP2=AC2,有:
2x2-2x+5=5,解得x=0(舍去),x=1,
∴P2(1,-2);
③当CP=AC时,CP2=AC2,有:
2x2=5,解得x=±
,
∴P3(
,-
-1),P4(-
,
-1);
综上所述,存在符合条件的P点,且P点坐标为:P1(2.5,-3.5)、P2(1,-2)、P3(
,-
-1)、P4(-
,
-1).
代入点B(-1,0)、C(0,-1),
求得y=-x-1;
设P(x,-x-1),因为A(2,0),C(0,-1),则有:
AP2=(x-2)2+(-x-1)2=2x2-2x+5,
AC2=5,CP2=x2+(-x-1+1)2=2x2;
①当AP=CP时,AP2=CP2,有:
2x2-2x+5=2x2,解得x=2.5,
∴P1(2.5,-3.5);
②当AP=AC时,AP2=AC2,有:
2x2-2x+5=5,解得x=0(舍去),x=1,
∴P2(1,-2);
③当CP=AC时,CP2=AC2,有:
2x2=5,解得x=±
| ||
| 2 |
∴P3(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
综上所述,存在符合条件的P点,且P点坐标为:P1(2.5,-3.5)、P2(1,-2)、P3(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:此题考查等腰三角形的判定与性质,同时还考查了分类讨论、数形结合的数学思想.

练习册系列答案
相关题目
 一个正方体每个面都写有一个汉字,其平面展开如图所示,那么在该正方体中,和“大”字向对面上所写的字是( )
一个正方体每个面都写有一个汉字,其平面展开如图所示,那么在该正方体中,和“大”字向对面上所写的字是( )| A、中 | B、国 | C、的 | D、梦 |
已知二次函数y=x2-2x+1,当y=4时,x的值等于( )
| A、3和-1 | B、-3和1 |
| C、3和1 | D、-3和-1 |
 如图,某商场为吸引顾客,开展有奖促销活动,设计了如图两个转盘,转盘1被分成3个面积相等的扇形,分别标有字母A、B、C;转盘2被分成2个半圆,分别标有字母C、D,规定:游戏者分别转动如图的两个可以自由转动的转盘各一次,当两个转盘的指针所指字母都相同时,他就可以获得一张100元购物券的机会.
如图,某商场为吸引顾客,开展有奖促销活动,设计了如图两个转盘,转盘1被分成3个面积相等的扇形,分别标有字母A、B、C;转盘2被分成2个半圆,分别标有字母C、D,规定:游戏者分别转动如图的两个可以自由转动的转盘各一次,当两个转盘的指针所指字母都相同时,他就可以获得一张100元购物券的机会.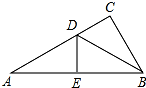 如图,Rt△ABC中,∠C=90°,AB=5,BC=3,D、E分别是AC、AB上的点,且△ADE沿DE折叠后,点A恰好落在点B处,则CD+BD的长为
如图,Rt△ABC中,∠C=90°,AB=5,BC=3,D、E分别是AC、AB上的点,且△ADE沿DE折叠后,点A恰好落在点B处,则CD+BD的长为 直线AB、CD相交于点O,OE平分∠AOC,∠FOD=90°,∠2:∠3=8:11,求∠1和∠EOF的度数.
直线AB、CD相交于点O,OE平分∠AOC,∠FOD=90°,∠2:∠3=8:11,求∠1和∠EOF的度数.