题目内容
已知⊙O的直径AB=10,弦BC=6,点D在⊙O上(与点C在AB两侧),过D作⊙O的切线PD.
(1)如图①,PD与AB的延长线交于点P,连接PC,若PC与⊙O相切,求弦AD的长;
(2)如图②,若PD∥AB,①求证:CD平分∠ACB;②求弦AD的长.
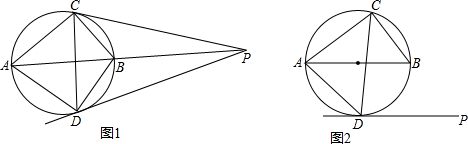
(1)如图①,PD与AB的延长线交于点P,连接PC,若PC与⊙O相切,求弦AD的长;
(2)如图②,若PD∥AB,①求证:CD平分∠ACB;②求弦AD的长.

考点:切线的性质,全等三角形的判定与性质,勾股定理
专题:
分析:(1)先求得∠ACB=90°,根据勾股定理求得AC,根据切线的性质求得PD=PC,∠APC=∠APD,然后根据SAS求得△APC≌△APD,即可求得AD=AC=8;
(2)连接OD、BD,根据切线的性质得出OD⊥PD,进而求得OD⊥AB,根据垂直平分线的性质求得AD=BD,从而求得CD平分∠ACB.根据勾股定理即可求得弦AD的长.
(2)连接OD、BD,根据切线的性质得出OD⊥PD,进而求得OD⊥AB,根据垂直平分线的性质求得AD=BD,从而求得CD平分∠ACB.根据勾股定理即可求得弦AD的长.
解答: (1)解:∵AB是⊙O的直径,
(1)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC=
=
=8,
∵PD、PC是⊙O的切线,
∴PD=PC,∠APC=∠APD,
在△APC和△APD中,
,
∴△APC≌△APD(SAS),
∴AD=AC=8.
(2)证明:①连接OD、BD,
∵PD是⊙O的切线,
∴OD⊥PD,
∵PD∥AB,
∴OD⊥AB,
∴
=
,
∴AD=BD,∠ACD=∠BCD,
∴CD平分∠ACB.
②∵AB是⊙O的直径,
∴∠ADB=90°,
在RT△ADB中,AD2+BD2=AB2,
∴2AD2=102,
∴AD=5
.
 (1)解:∵AB是⊙O的直径,
(1)解:∵AB是⊙O的直径,∴∠ACB=90°,
∴AC=
| AB2-BC2 |
| 102-62 |
∵PD、PC是⊙O的切线,
∴PD=PC,∠APC=∠APD,
在△APC和△APD中,
|
∴△APC≌△APD(SAS),
∴AD=AC=8.
(2)证明:①连接OD、BD,

∵PD是⊙O的切线,
∴OD⊥PD,
∵PD∥AB,
∴OD⊥AB,
∴
 |
| AD |
 |
| BD |
∴AD=BD,∠ACD=∠BCD,
∴CD平分∠ACB.
②∵AB是⊙O的直径,
∴∠ADB=90°,
在RT△ADB中,AD2+BD2=AB2,
∴2AD2=102,
∴AD=5
| 2 |
点评:本题考查了切线的性质,全等三角形的判定和性质,圆周角的性质,勾股定理的应用,也考查了切线长定理和等腰三角形的性质.

练习册系列答案
相关题目
方程x2=4的解为( )
| A、x=2 |
| B、x=-2 |
| C、x1=4,x2=-4 |
| D、x1=2,x2=-2 |
 一个正方体每个面都写有一个汉字,其平面展开如图所示,那么在该正方体中,和“大”字向对面上所写的字是( )
一个正方体每个面都写有一个汉字,其平面展开如图所示,那么在该正方体中,和“大”字向对面上所写的字是( )| A、中 | B、国 | C、的 | D、梦 |
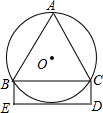 如图,△ABC是⊙O的内接等边三角形,矩形BCDE的边DE与⊙O相切,BE=3,则矩形BCDE的面积是( )
如图,△ABC是⊙O的内接等边三角形,矩形BCDE的边DE与⊙O相切,BE=3,则矩形BCDE的面积是( )| A、18 | ||
| B、9 | ||
C、18
| ||
D、9
|
如果⊙O的半径是4,线段OP的长为3,则点P( )
| A、在⊙O上 |
| B、在⊙O内 |
| C、在⊙O外 |
| D、在⊙O上或⊙O内 |
 直线AB、CD相交于点O,OE平分∠AOC,∠FOD=90°,∠2:∠3=8:11,求∠1和∠EOF的度数.
直线AB、CD相交于点O,OE平分∠AOC,∠FOD=90°,∠2:∠3=8:11,求∠1和∠EOF的度数.