题目内容
12.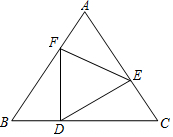 在△ABC中,己知AB=AC,点D、E、F分别在边BC、AC、AB上,且BD=CE,∠FDE=∠B,
在△ABC中,己知AB=AC,点D、E、F分别在边BC、AC、AB上,且BD=CE,∠FDE=∠B,(1)说明△BFD与△CDE全等的理由;
(2)如果△ABC是等边三角形,那么△DEF是等边三角形吗?试说明理由.
分析 (1)利用AB=AC得到∠B=∠C,再利用三角形外角性质证明∠EDC=∠BFD,然后根据“AAS”证明△BDF≌△CED;
(2)根据等边三角形的性质得∠B=60°,再利用全等的性质得DF=ED,加上∠FDE=∠B=60°,然后根据等边三角形的判定方法可判断△DEF是等边三角形.
解答 (1)证明:∵AB=AC,
∴∠B=∠C,
∵∠FDC=∠B+∠BFD,
而∠FDE=∠B,
∴∠EDC=∠BFD,
在△BDF和△CED中
$\left\{\begin{array}{l}{∠BFD=∠CDE}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$,
∴△BDF≌△CED;
(2)解:△DEF是等边三角形.理由如下:
∵△ABC是等边三角形,
∴∠B=60°
∵△BDF≌△CED,
∴DF=ED,
∵∠FDE=∠B=60°,
∴△DEF是等边三角形.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
3.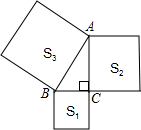 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )
如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )
 如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )
如图,以Rt△ABC的三边为边向外作正方形,其面积分别为S1,S2,S3,且S1=64,S3=289,则S2为( )| A. | 15 | B. | 225 | C. | 81 | D. | 25 |
20.如果a的立方根等于a,那么a的值为( )
| A. | 0 | B. | 0或1 | C. | 0或-1 | D. | 0或±1 |
4.若方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标,则k的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | ±2 |
1.点(-1,a2+1)一定在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.点A(2,y1)、B(3,y2)都在一次函数y=-2x+3的图象上,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
 如图,在正方形ABCD中,点E在边AD上,以DE为对角线构造正方形DGEF,点G在正方形ABCD内部,连接BF与边AD交于点M,连接CG.若DM=6,AM=4,则线段CG的长为$\frac{50}{7}$.
如图,在正方形ABCD中,点E在边AD上,以DE为对角线构造正方形DGEF,点G在正方形ABCD内部,连接BF与边AD交于点M,连接CG.若DM=6,AM=4,则线段CG的长为$\frac{50}{7}$.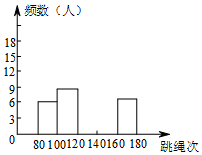 体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示: 如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,试判断AO与BC的位置关系.
如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,试判断AO与BC的位置关系.