题目内容
2. 如图,在正方形ABCD中,点E在边AD上,以DE为对角线构造正方形DGEF,点G在正方形ABCD内部,连接BF与边AD交于点M,连接CG.若DM=6,AM=4,则线段CG的长为$\frac{50}{7}$.
如图,在正方形ABCD中,点E在边AD上,以DE为对角线构造正方形DGEF,点G在正方形ABCD内部,连接BF与边AD交于点M,连接CG.若DM=6,AM=4,则线段CG的长为$\frac{50}{7}$.
分析 连接AF,过F作FH⊥AD于H,根据△ADF≌△CDG,可得CG=AF,设FH=DH=x,则MH=6-x,根据FH∥AB,可得$\frac{FH}{BA}$=$\frac{MH}{MA}$,即$\frac{x}{10}$=$\frac{6-x}{4}$,求得FH=$\frac{30}{7}$,MH=$\frac{12}{7}$,AH=$\frac{40}{7}$,再根据勾股定理即可得到Rt△AFH中AF的长,进而得出CG的长.
解答 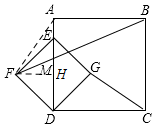 解:如图,连接AF,过F作FH⊥AD于H,则FH∥AB,
解:如图,连接AF,过F作FH⊥AD于H,则FH∥AB,
∵四边形ABCD和四边形DFEG是正方形,
∴DF=DG,∠ADF=∠ADG=45°=∠CDG,AD=CD,
∴△ADF≌△CDG,
∴CG=AF,
∵DM=6,AM=4,
∴AB=10,
设FH=DH=x,则MH=6-x,
∵FH∥AB,
∴$\frac{FH}{BA}$=$\frac{MH}{MA}$,即$\frac{x}{10}$=$\frac{6-x}{4}$,
解得x=$\frac{30}{7}$,
∴FH=$\frac{30}{7}$,MH=$\frac{12}{7}$,AH=$\frac{40}{7}$,
∴Rt△AFH中,AF=$\sqrt{(\frac{40}{7})^{2}+(\frac{30}{7})^{2}}$=$\frac{50}{7}$,
∴CG=$\frac{50}{7}$,
故答案为:$\frac{50}{7}$.
点评 本题考查了正方形的性质、平行线分线段成比例定理、勾股定理等知识的综合应用,解题的关键是添加辅助线构造直角三角形,利用勾股定理解决问题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 如图:在等腰Rt△ABC中,BD=AE,BF与DE垂直,求证:ED=BF.
如图:在等腰Rt△ABC中,BD=AE,BF与DE垂直,求证:ED=BF. 如图,A、C、F、B在同一直线上,AC=BF,AE=BD,且∠A=∠B.求证:EF∥CD.
如图,A、C、F、B在同一直线上,AC=BF,AE=BD,且∠A=∠B.求证:EF∥CD.
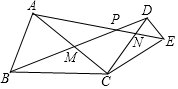 如图,△ABC和△DCE均为等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.
如图,△ABC和△DCE均为等腰三角形,CA=CB,CD=CE,∠BCA=∠DCE.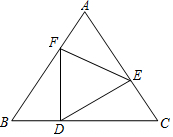 在△ABC中,己知AB=AC,点D、E、F分别在边BC、AC、AB上,且BD=CE,∠FDE=∠B,
在△ABC中,己知AB=AC,点D、E、F分别在边BC、AC、AB上,且BD=CE,∠FDE=∠B,