题目内容
17. 如图,Rt△ABC中,∠C=90°,tanB=$\frac{1}{4}$,AD是BC边上的中线,则sin∠BAD=$\frac{2\sqrt{85}}{85}$.
如图,Rt△ABC中,∠C=90°,tanB=$\frac{1}{4}$,AD是BC边上的中线,则sin∠BAD=$\frac{2\sqrt{85}}{85}$.
分析 作高线DE,证明△DEB∽△ACB,求DE的长,再利用三角函数定义求结果.
解答 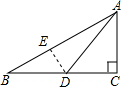 解:∵∠C=90°,tanB=$\frac{1}{4}$,
解:∵∠C=90°,tanB=$\frac{1}{4}$,
∴设AC=k,BC=4k,
∴AB=$\sqrt{17}$k,
∵AD是BC边上的中线,
∴BD=CD=2k,
过点D作DE⊥AB于E,
∴∠C=∠DEB=90°,
又∠B=∠B,
∴△DEB∽△ACB,
∴$\frac{DE}{AC}$=$\frac{BD}{AB}$,
∴$\frac{DE}{k}=\frac{2k}{\sqrt{17}k}$,
∴DE=$\frac{2\sqrt{17}}{17}$k,
∵AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{5}$k,
∴sin∠BAD=$\frac{DE}{AD}$=$\frac{\frac{2\sqrt{17}}{17}k}{\sqrt{5}k}$=$\frac{2\sqrt{85}}{85}$.
故答案为:$\frac{2\sqrt{85}}{85}$.
点评 本题考查了解直角三角形,熟练掌握直角三角形的边角关系是解题的关键.

练习册系列答案
相关题目
9.半径为2的圆内有两条互相垂直的弦AB和CD,它们的交点E到圆心O的距离等于1,则AB2+CD2=( )
| A. | 28 | B. | 26 | C. | 18 | D. | 35 |
6. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )
 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=8,则CP的长为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
7.甲、乙两名工人同时加工同一种零件,现根据两人7天产品中每天出现的次品数情况制成如下统计表,依据相关信息,解答下列问题:
(1)在统计表中,工人甲7天出现次品数的众数为2,其极差是4,工人乙7天出现次品数的中位数为1;
(2)根据题目所给数据,通过计算判断甲、乙两名工人谁出现次品的波动要小些;
(3)请估计甲、乙加工该种零件30天共出现次品多少件?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 甲(件) | 2 | 2 | 0 | 3 | 1 | 2 | 4 |
| 乙(件) | 1 | 0 | 2 | 1 | 1 | 0 | 2 |
(2)根据题目所给数据,通过计算判断甲、乙两名工人谁出现次品的波动要小些;
(3)请估计甲、乙加工该种零件30天共出现次品多少件?

 如图,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,坡角A为30°,坝高DE=8m,坝底宽AB为(27+8$\sqrt{3}$)m,试求迎水坡BC的长和迎水坡BC的坡度.
如图,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,坡角A为30°,坝高DE=8m,坝底宽AB为(27+8$\sqrt{3}$)m,试求迎水坡BC的长和迎水坡BC的坡度.