题目内容
20.计算:$\sqrt{(-3{)^2}}-(\frac{1}{4}{)^{-1}}+\sqrt{2}•cos{45°}$的结果为0.分析 首先根据平方根的计算方法,求出$\sqrt{{(-3)}^{2}}$的值是多少;然后根据负整数指数幂:a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数),求出${(\frac{1}{4})}^{-1}$的大小;再根据$cos45°=\frac{\sqrt{2}}{2}$,求出$\sqrt{2}cos45°$的大小;最后从左向右依次计算,求出算式$\sqrt{(-3{)^2}}-(\frac{1}{4}{)^{-1}}+\sqrt{2}•cos{45°}$的结果是多少即可.
解答 解:$\sqrt{(-3{)^2}}-(\frac{1}{4}{)^{-1}}+\sqrt{2}•cos{45°}$
=3$-4+\sqrt{2}×\frac{\sqrt{2}}{2}$
=3-4+1
=0
故答案为:0.
点评 此题主要考查了平方根、负整数指数幂和特殊角的三角函数值的求法,要熟练掌握运算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.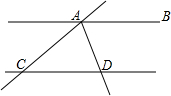 如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )
如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )
 如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )
如图,AB∥CD,AD平分∠BAC,若∠ADC=70°,则∠ACD的度数为( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
8. 如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
 如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )| A. | $\frac{9}{2}$ | B. | $\frac{27}{4}$ | C. | $\frac{24}{5}$ | D. | 12 |
15.一艘轮船以18海里/时沿北偏东60°的方向航行,上午九时,测得小岛A在正东方向,3小时后,看见小岛在南偏东30°方向上,此时船与小岛的距离为( )
| A. | 27$\sqrt{2}$海里 | B. | 18$\sqrt{3}$海里 | C. | 27$\sqrt{3}$海里 | D. | 18$\sqrt{2}$海里 |
12.-$\frac{1}{5}$的绝对值是( )
| A. | 5 | B. | -5 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
9.($\frac{1}{2}$)2的相反数是( )
| A. | 4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | -4 |
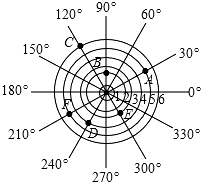 如图,雷达探测器测得六个目标A、B、C、D、E、F出现,按照规定的目标表示方法,目标A、E的位置表示为A(5,30°),E(3,300°),则目标C的位置表示为(6,120°).
如图,雷达探测器测得六个目标A、B、C、D、E、F出现,按照规定的目标表示方法,目标A、E的位置表示为A(5,30°),E(3,300°),则目标C的位置表示为(6,120°).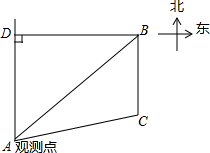 已知B村庄位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为24km,一辆摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此摩托车与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,$\sqrt{2}$≈1.41,$\sqrt{5}$≈2.24.
已知B村庄位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为24km,一辆摩托车从B村庄以60km/h的速度沿如图所示的BC方向航行,15min后达到C处,现测得C处位于A观测点北偏东79.8°方向,求此摩托车与A观测点之间的距离AC的长(精确到0.1km).(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,$\sqrt{2}$≈1.41,$\sqrt{5}$≈2.24.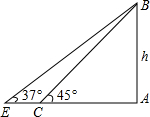 如图,数学课外活动小组测电视塔AB的高度,他们在点C处测得塔顶B的仰角为45°,自C点沿AC方向前进40米到达点E,在点E处测得B的仰角为37°(A、C、E三点在一条直线上).求电视塔的高度h.(结果精确到0.1米,参考数据:sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)
如图,数学课外活动小组测电视塔AB的高度,他们在点C处测得塔顶B的仰角为45°,自C点沿AC方向前进40米到达点E,在点E处测得B的仰角为37°(A、C、E三点在一条直线上).求电视塔的高度h.(结果精确到0.1米,参考数据:sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)