题目内容
19.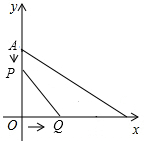 如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.
如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.(1)求运动时间t的取值范围;
(2)t为何值时,△POQ的面积最大?最大值是多少?
(3)t为何值时,以点P、0、Q为顶点的三角形与Rt△AOB相似?
分析 (1)由点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动,可得:2t=8,解得:t=4,进而可得:0≤t≤4;
(2)先根据三角形的面积公式,用含有t的式子表示△POQ的面积=-t2+6t,然后根据二次函数的最值公式解答即可;
(3)分两种情况讨论:①Rt△POQ∽Rt△AOB;②Rt△QOP∽Rt△AOB,然后根据相似三角形对应边成比例,即可求出相应的t的值.
解答 解:(1)∵点A(0,6),B(8,0),
∴OA=6,OB=8,
∵点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动,
∴2t=8,
解得:t=4,
∴0≤t≤4;
(2)根据题意得:经过t秒后,AP=t,OQ=2t,
∴OP=OA-AP=6-t,
∵△POQ的面积=$\frac{1}{2}$•OP•OQ,
即△POQ的面积=$\frac{1}{2}×$(6-t)×2t=-t2+6t.
∵a=-1<0,
∴△POQ的面积有最大值,
当t=-$\frac{b}{2a}$=3时,△POQ的面积的最大值=$\frac{4ac-{b}^{2}}{4a}$=9,
即当t=3时,△POQ的面积最大,最大值是9.
(3)①若Rt△POQ∽Rt△AOB时,
∵Rt△POQ∽Rt△AOB,
∴$\frac{PO}{AO}=\frac{OQ}{OB}$,
即$\frac{6-t}{6}$=$\frac{2t}{8}$,
解得:t=$\frac{12}{5}$;
②若Rt△QOP∽Rt△AOB时,
∵Rt△QOP∽Rt△AOB,
∴$\frac{OQ}{AO}=\frac{OP}{OB}$,
即$\frac{2t}{6}=\frac{6-t}{8}$,
解得:t=$\frac{18}{11}$.
所以当t为$\frac{12}{5}$或$\frac{18}{11}$时,以点P、0、Q为顶点的三角形与Rt△AOB相似.
点评 此题是一次函数的综合题型,主要考查了三角形的面积,二次函数的最值,相似三角形的判定与性质,第(3)问的解题的关键是:分两种情况讨论:①Rt△POQ∽Rt△AOB;②Rt△QOP∽Rt△AOB.

| A. | 4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | -4 |
| A. | ±3 | B. | -3 | C. | 3 | D. | ±81 |
| A. | $\frac{17}{2}$ | B. | $\frac{17}{4}$ | C. | $\frac{19}{2}$ | D. | $\frac{19}{4}$ |
| A. | 2a3•a4=2a7 | B. | 2(a+1)=2a+1 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |
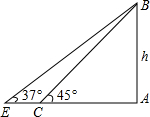 如图,数学课外活动小组测电视塔AB的高度,他们在点C处测得塔顶B的仰角为45°,自C点沿AC方向前进40米到达点E,在点E处测得B的仰角为37°(A、C、E三点在一条直线上).求电视塔的高度h.(结果精确到0.1米,参考数据:sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)
如图,数学课外活动小组测电视塔AB的高度,他们在点C处测得塔顶B的仰角为45°,自C点沿AC方向前进40米到达点E,在点E处测得B的仰角为37°(A、C、E三点在一条直线上).求电视塔的高度h.(结果精确到0.1米,参考数据:sin37°≈$\frac{3}{5}$,cos37°≈$\frac{4}{5}$,tan37°≈$\frac{3}{4}$)