Question

阅读理解：课本在研究“圆周角和圆心角的关系”时，有以下内容．
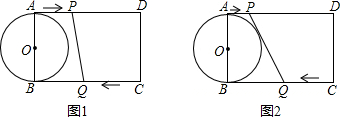
【议一议】如图1，其中O为圆心，观察圆周角∠ABC与圆心角∠AOC，它们的大小有什么关系？说说你的想法，并与同伴交流．小亮首先考虑了一种特殊情况，即∠ABC的一边BC经过圆心O（图2）．
∵∠AOC是△ABO的外角，
∴∠AOC=∠ABO+∠BAO．
∵OA=OB，
∴∠ABO=∠BAO．
∴∠AOC=2∠ABO，
即∠ABC=

1

2

∠AOC．

如果∠ABC的两边都不经过圆心O（图1，图3），那么结果会怎样？你能将图1与图3的两种情况分别转化成图2的情况去解决吗？
自主证明：请在图1和图3中选择一种情况解决上述问题（即∠ABC与∠AOC的大小关系），写出证明过程．
拓展探究：将图1中的弦AB绕点B旋转，当AB与⊙O相切时（图4），试探究∠ABC与∠BOC的大小关系？写出你的结论，并说明理由．

Answer 1

考点：圆的综合题

专题：探究型

分析：自主证明：连接BO，并延长BO交⊙O于点D，由小亮的证明知：∠ABD=

1

2

∠AOD，∠CBD=

1

2

∠COD，从而可以证到∠ABC=

1

2

∠AOC．
拓展探究：延长BO交⊙O于点E，连接EC，由小亮的证明知：∠BEC=

1

2

∠BOC．根据同角的余角相等可得∠ABC=∠BEC，从而得到∠ABC=

1

2

∠BOC．

解答：解：①连接BO，并延长BO交⊙O于点D，如图1，
由小亮的证明知：∠ABD=

1

2

∠AOD，∠CBD=

1

2

∠COD．
∴∠ABC=∠ABD+∠CBD
=

1

2

∠AOD+

1

2

∠COD
=

1

2

（∠AOD+∠COD）
=

1

2

∠AOC．
②连接BO，并延长BO交⊙O于点D，如图3，
由小亮的证明知：∠ABD=

1

2

∠AOD，∠CBD=

1

2

∠COD．
∴∠ABC=∠ABD-∠CBD
=

1

2

∠AOD-

1

2

∠COD
=

1

2

（∠AOD-∠COD）
=

1

2

∠AOC．
拓展探究：∠ABC=

1

2

∠BOC，
理由如下：
延长BO交⊙O于点E，连接EC，由小亮的证明知：∠BEC=

1

2

∠BOC．
∵BA与⊙O相切于点B，
∴∠ABO=90°，即∠ABC+∠CBO=90°．
又∵BE是⊙O的直径，
∴∠BCE=90°，即∠BEC+∠CBO=90°．
∴∠ABC=∠BEC，
∴∠ABC=

1

2

∠BOC．

点评：本题考查了切线的性质、圆周角定理、同角的余角相等等知识，考查了用已有经验解决问题的能力，渗透了转化思想，体现了自主探究与合作交流相结合的新课程理念，是一道好题．