题目内容
2.下面对关于x的一元二次方程a(x-1)2=2x2-2的表述错误的是( )| A. | 判别式的值为16 | B. | 方程有一根是1 | C. | a不等于0 | D. | a不等于2 |
分析 由一元二次方程的定义得到a-2≠0,即a≠2,求出△的值,对方程进行验根,即可得到结论.
解答 解:a(x-1)2=2x2-2可化为:(a-2)x2-2ax+a+2=0,
∵方程是一元二次方程,
∴a-2≠0,
即a≠2,
∵△=4a2-4(a-2)(a+2)=16,
把x=1代入(a-2)x2-ax+a+2=0,
则方程的左右两边相等,
故A,B,D正确,
故选C.
点评 此题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了一元二次方程的定义.

练习册系列答案
相关题目
10.下列说法错误的是( )
| A. | 若$\frac{x}{a}=\frac{y}{a}$,则x=y | B. | 若x2=y2,则-4x2=-4y2 | ||
| C. | 若-$\frac{1}{4}$x=6,则x=-$\frac{3}{2}$ | D. | 若6=-x,则x=-6 |
14.若a,b,c分别为三角形的三边,化简:|a-b-c|-|a-b+c|得( )
| A. | -2c | B. | 2b-2a | C. | 2a | D. | 2c-2a |
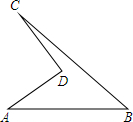 实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,若每平方米草皮需要300元,学校需要投入多少资金买草皮?
实验中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,若每平方米草皮需要300元,学校需要投入多少资金买草皮?