题目内容
17. 如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,α),点B(2,n)是反比例函数图象上一点,连接OB.
如图,直线y=2x与反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象交于点A(1,α),点B(2,n)是反比例函数图象上一点,连接OB.(1)求k的值及点B的坐标;
(2)求△OAB的面积;
(3)设点P(m,0),若△PAB的面积为2,求m的值.
分析 (1)把点A(1,a)代入直线y=2x,就可得到点A的坐标,把点A的坐标代入反比例函数的解析式可得到k,再把点B的坐标代入反比例函数解析式,就可求出点B的坐标;
(2)延长AB交x轴于点C,如图1,运用待定系数法可求出直线AB的解析式,从而可求出点C的坐标,然后运用割补法就可解决问题;
(3)运用割补法可求出PC的值,结合点C的坐标就可求出m的值.
解答 解:(1)∵点A(1,a)在直线y=2x上,
∴a=2×1=2,A(1,2).
∵A(1,2)在反比例函数y=$\frac{k}{x}$上,
∴k=1×2=2,y=$\frac{2}{x}$.
∵点B(2,n)是反比例函数y=$\frac{2}{x}$图象上,
∴n=$\frac{2}{2}$=1,B(2,1);
(2)延长AB交x轴于点C,如图1,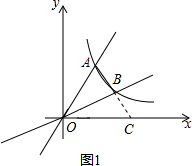
设直线AB的解析式为y=mx+n,
则有$\left\{\begin{array}{l}{m+n=2}\\{2m+n=1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-1}\\{n=3}\end{array}\right.$,
∴直线AB的解析式为y=-x+3.
∵点C是直线y=-x+3与x轴的交点,
∴点C的坐标为(3,0),OC=3,
∴S△OAB=S△OAC-S△OBC
=$\frac{1}{2}$×3×2-$\frac{1}{2}$×3×1=$\frac{3}{2}$;
(3)如图2,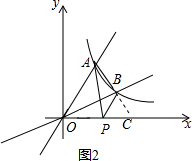
∵S△PAB=2,
∴S△PAB=S△PAC-S△PBC=$\frac{1}{2}$×PC×2-$\frac{1}{2}$×PC×1=$\frac{1}{2}$PC=2,
∴PC=4.
∵C(3,0),P(m,0),
∴$|\begin{array}{l}{m-3}\end{array}|$=4,
∴m=-1或7.
点评 本题主要考查了运用待定系数法求直线及反比例函数的解析式、运用割补法求三角形的面积等知识,运用割补法是解决本题的关键,需要注意的是线段的长度确定,点的坐标未必确定.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案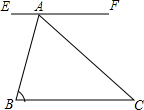 如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是( )
如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是( )| A. | 70° | B. | 60° | C. | 55° | D. | 50° |
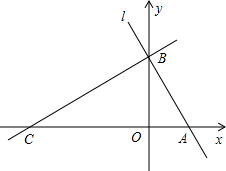 如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点,点A的坐标为(1,0)∠ABO=30°,过点B的直线y=$\frac{{\sqrt{3}}}{3}$x+m与x轴交于点C.
如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点,点A的坐标为(1,0)∠ABO=30°,过点B的直线y=$\frac{{\sqrt{3}}}{3}$x+m与x轴交于点C.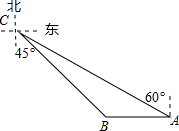 如图,码头A在码头B的正东方向,两个码头之间的距离为20海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.($\sqrt{3}$≈1.732,结果精确到0.1海里)
如图,码头A在码头B的正东方向,两个码头之间的距离为20海里,今有一货船由码头A出发,沿北偏西60°方向航行到达小岛C处,此时测得码头B在南偏东45°方向,求码头A与小岛C的距离.($\sqrt{3}$≈1.732,结果精确到0.1海里)