��Ŀ����
9��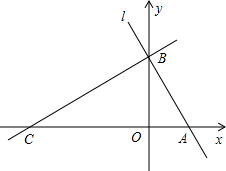 ��ͼ��ƽ��ֱ������ϵ�У�ֱ��l�ֱ�x�ᡢy����A��B���㣬��A������Ϊ��1��0����ABO=30�㣬����B��ֱ��y=$\frac{{\sqrt{3}}}{3}$x+m��x�ύ�ڵ�C��
��ͼ��ƽ��ֱ������ϵ�У�ֱ��l�ֱ�x�ᡢy����A��B���㣬��A������Ϊ��1��0����ABO=30�㣬����B��ֱ��y=$\frac{{\sqrt{3}}}{3}$x+m��x�ύ�ڵ�C����1����ֱ��l�Ľ���ʽ����C�����꣮
��2����D��x���ϴӵ�C���A��ÿ��1����λ�����ٶ��˶���0��t��4��������D�ֱ���DE��AB��DF��BC����BC��AB�ڵ�E��F������EF����GΪEF���е㣮
���ж��ı���DEBF����״��֤���������tΪ��ֵʱ�߶�DG�ij���̣�
��3����P��y���ϵĵ㣬������ƽ�����Ƿ���ڵ�Q��ʹ��A��B��P��QΪ������ı��������Σ������ڣ���ֱ��д��Q������ꣻ�������ڣ�˵�����ɣ�
���� ��1��������һ����Ϊ30���ֱ�������ε����ʣ����OB�������ô���ϵ����������⣻
��2������һ������ֱ�ǵ�ƽ���ı����Ǿ��Σ��жϳ��ı���DEBF�Ǿ��Σ������õ㵽ֱ�ߵľ����д��߶���̼��ɣ�
��3�������P��0��m�������꣬������ƽ���ı��ε���������ͼ�Σ������Q�����꣬���������ε��ı�������m���ɣ�
��� ��1���⣺��A��1��0����
��OA=1��
�ߡ�ABO=30�㣬
��0B=$\sqrt{3}$��AB=2��
��B��O��$\sqrt{3}$����
��ֱ��l�Ľ���ʽΪy=kx+$\sqrt{3}$��
��A��1��0����ֱ��l�ϣ�
��k=-$\sqrt{3}$��
��y=-$\sqrt{3}$x+$\sqrt{3}$��
��B��0��$\sqrt{3}$����ֱ��y=$\frac{\sqrt{3}}{3}$x+m�ϣ�
��m=$\sqrt{3}$��
��ֱ��BC�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$��
�ߵ�C��x���ϣ�
��C-3��0����
��2���⣺��ͼ1��
���ı���DEBFΪ���Σ�
��DE��AB��DF��BC��
���ı���BEDFΪƽ���ı��Σ�
��ƽ���ı���BEDFΪ���Σ�
�ڡ�GΪEF�е㣬
��GΪ����BEDF�ĶԽ��ߵĽ��㣬
��ҪʹDG��̣�Ҳ����BD��̣�
��ֻ��BD��ACʱ��BD��̣�
��CD=3��
��t=3��
��3��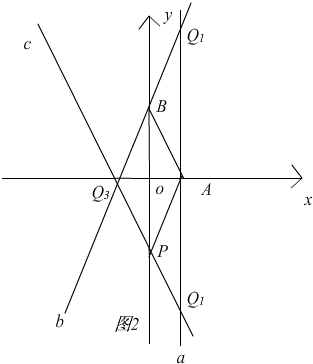
�⣺��ͼ2��������ƽ�����Ǵ��ڵ�Q��ʹ��A��B��P��QΪ������ı��������Σ�
��P��0��m����A��1��0����B��0��$\sqrt{3}$����
��ֱ��AB�Ľ���ʽΪy=-$\sqrt{3}$x+$\sqrt{3}$��
��a��BP����ֱ��a�Ľ���ʽΪx=1��
��b��AP����ֱ��b�Ľ���ʽΪy=mx+$\sqrt{3}$��
��c��AB����ֱ��c�Ľ���ʽΪy=-$\sqrt{3}$x+m��
����ABΪ�Խ���ʱ����$\left\{\begin{array}{l}{x=1}\\{y=-mx+\sqrt{3}}\end{array}\right.$��
��Q1��1��-m+$\sqrt{3}$����
���ı���Q1BPAΪ���Σ�
��Q1A=Q1B������Q1A2=Q1B2��
�ࣨ-m+$\sqrt{3}$��2=1+m2��
��m=$\frac{\sqrt{3}}{3}$��
��Q1��1��$\frac{2\sqrt{3}}{3}$����P��0��$\frac{\sqrt{3}}{3}$����
����ABΪ��ʱ��
��QPΪ�Խ���ʱ��
�ߵ�A��1��0����B��0��$\sqrt{3}$����
��AB=2��
�ߵ�P��y���ϵĵ㣬
��P��0��$\sqrt{3}$+2����P��0��$\sqrt{3}$-2��
��AB����ʽΪy=-$\sqrt{3}$x+$\sqrt{3}$��
��AP����ʽΪy=-$\sqrt{3}$x+$\sqrt{3}$+2��y=-$\sqrt{3}$x+$\sqrt{3}$-2��
���ı���APQBΪ���Σ�
���Q����A��PQ��y���ֱ���ϣ�
��Q2��1��2����Q3��1��-2����
����BPΪ�Խ���ʱ��
��P��0��-$\sqrt{3}$����
���Q4��-1��0����
����ڵ�Q��ʹ��A��B��P��QΪ������ı��������Σ�Q1��1��$\frac{2\sqrt{3}}{3}$������Q2��1��2������Q3��1��-2����Q4��-1��0����
���� ������һ�κ����м��ۺ��⣬�漰������ϵ������ֱ�߽���ʽ��ƽ��������֮����빫ʽ�����÷�������ֱ�ߵĽ������꣬�Ȿ��Ĺؼ���������ֱ��ƽ�У�����ϵ����ȣ����ֱ�߽���ʽ��ֱ��AB�Ľ���ʽΪy=-$\sqrt{3}$x+$\sqrt{3}$��ֱ��AB�Ľ���ʽΪy=-mx+m����a��BP����ֱ��a�Ľ���ʽΪx=1����b��AP����ֱ��b�Ľ���ʽΪy=mx+$\sqrt{3}$����c��AB����ֱ��c�Ľ���ʽΪy=-$\sqrt{3}$x+m��

| A�� | 6 | B�� | 5 | C�� | 4 | D�� | 3 |
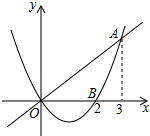 ��ͼ����֪���κ���y1=$\frac{2}{3}$x2-$\frac{4}{3}$x��ͼ��������������y2=$\frac{2}{3}$x��ͼ���ڵ�A��3��2������x�ύ�ڵ�B��2��0������y1��y2����x��ȡֵ��Χ�ǣ�������
��ͼ����֪���κ���y1=$\frac{2}{3}$x2-$\frac{4}{3}$x��ͼ��������������y2=$\frac{2}{3}$x��ͼ���ڵ�A��3��2������x�ύ�ڵ�B��2��0������y1��y2����x��ȡֵ��Χ�ǣ�������| A�� | 0��x��2 | B�� | 0��x��3 | C�� | 2��x��3 | D�� | x��0��x��3 |
 ��ͼ��O����ֱ��AB�ϣ���AOD=90�㣬��COE=90�㣬��ͼ����ȵ������2�ԣ�
��ͼ��O����ֱ��AB�ϣ���AOD=90�㣬��COE=90�㣬��ͼ����ȵ������2�ԣ� ��ͼ��ֱ��y=2x�뷴��������y=$\frac{k}{x}$��k��0��x��0����ͼ���ڵ�A��1����������B��2��n���Ƿ���������ͼ����һ�㣬����OB��
��ͼ��ֱ��y=2x�뷴��������y=$\frac{k}{x}$��k��0��x��0����ͼ���ڵ�A��1����������B��2��n���Ƿ���������ͼ����һ�㣬����OB��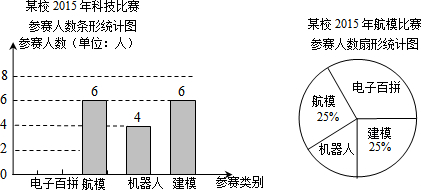
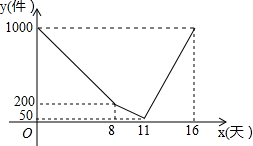 ij���ҿ���һ���²�Ʒ������һ���Ŀ������Ͷ���г��������������ڼ䲻�����������������ҿ�ʼ��ʽͶ�������������������ʱ����������˹���Ч�ʣ��ò�Ʒÿ�����������ͬʱ�������y������������������x��֮��ĺ�����ϵ��ͼ��ʾ�������=ԭ�п����+��������-����������
ij���ҿ���һ���²�Ʒ������һ���Ŀ������Ͷ���г��������������ڼ䲻�����������������ҿ�ʼ��ʽͶ�������������������ʱ����������˹���Ч�ʣ��ò�Ʒÿ�����������ͬʱ�������y������������������x��֮��ĺ�����ϵ��ͼ��ʾ�������=ԭ�п����+��������-����������