题目内容
16.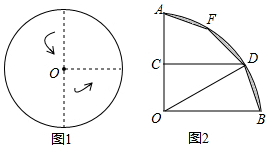 如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交$\widehat{AB}$于点D,点F是$\widehat{AB}$上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为36π-108.
如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交$\widehat{AB}$于点D,点F是$\widehat{AB}$上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为36π-108.
分析 先求出∠ODC=∠BOD=30°,作DE⊥OB可得DE=$\frac{1}{2}$OD=3,先根据S弓形BD=S扇形BOD-S△BOD求得弓形的面积,再利用折叠的性质求得所有阴影部分面积.
解答 解:如图,∵CD⊥OA,
∴∠DCO=∠AOB=90°,
∵OA=OD=OB=6,OC=$\frac{1}{2}$OA=$\frac{1}{2}$OD,
∴∠ODC=∠BOD=30°,
作DE⊥OB于点E,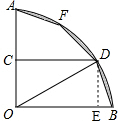
则DE=$\frac{1}{2}$OD=3,
∴S弓形BD=S扇形BOD-S△BOD=$\frac{30•π•{6}^{2}}{360}$-$\frac{1}{2}$×6×3=3π-9,
则剪下的纸片面积之和为12×(3π-9)=36π-108,
故答案为:36π-108.
点评 本题主要考查扇形面积的计算,熟练掌握扇形的面积计算公式及折叠的性质是解题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
11.甲、乙、丙、丁四人进行射击测试,记录每人10次射击成绩,得到各人的射击成绩平均数和方差如表中所示,则成绩最稳定的是( )
| 统计量 | 甲 | 乙 | 丙 | 丁 |
| 平均数 | 9.2 | 9.2 | 9.2 | 9.2 |
| 方差 | 0.60 | 0.62 | 0.50 | 0.44 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
5.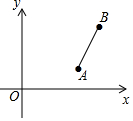 已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )
已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )
 已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )
已知A(4,1),B(5,4),将线段AB绕点A逆时针旋转90°得线段AC,则点C的坐标为( )| A. | (1,2) | B. | (2,1) | C. | (7,0) | D. | (1,3) |
 已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|=7.
已知在没有标明原点的数轴上有四个点,且它们表示的数分别为a、b、c、d.若|a-c|=10,|a-d|=12,|b-d|=9,则|b-c|=7.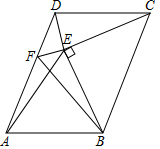 如图,在?ABCD中,以BC为斜边在?ABCD内作等腰直角△BCE,连接DE,过点E作EF⊥DE交AD于点F,∠CDE=∠CED=∠DCB.
如图,在?ABCD中,以BC为斜边在?ABCD内作等腰直角△BCE,连接DE,过点E作EF⊥DE交AD于点F,∠CDE=∠CED=∠DCB.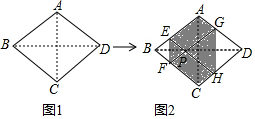 如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断: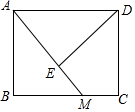 如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为$\frac{2\sqrt{5}}{5}$.
如图,在矩形ABCD中,M为BC边上一点,连接AM,过点D作DE⊥AM,垂足为E.若DE=DC=1,AE=2EM,则BM的长为$\frac{2\sqrt{5}}{5}$.