题目内容
11.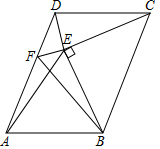 如图,在?ABCD中,以BC为斜边在?ABCD内作等腰直角△BCE,连接DE,过点E作EF⊥DE交AD于点F,∠CDE=∠CED=∠DCB.
如图,在?ABCD中,以BC为斜边在?ABCD内作等腰直角△BCE,连接DE,过点E作EF⊥DE交AD于点F,∠CDE=∠CED=∠DCB.(1)若BC=2$\sqrt{2}$,求AE的长;
(2)连接FB,求证:EF+FA=FB.
分析 (1)首先证明∠DCE=30°,推出△AEB是等边三角形,由此即可解决问题;
(2)在FD上取一点H,使得FH=FE.先证明△FHE是等边三角形,再证明△HEA≌△FEB即可解决问题;
解答 (1)解:在Rt△BCE中,∵CE=EB,BC=2$\sqrt{2}$,
∴EC=EB=2,设∠CDE=∠CED=∠DCB=x,
则有:45°+$\frac{1}{2}$(180°-2x)=x,
解得x=75°,
∴∠DCB=30°,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠ABC=180°-∠DCB=120°,
∵∠EBC=45°,
∴∠ABE=60°,
∵CD=CE=EB=AB,
∴△AEB是等边三角形,
∴AE=BE=2.
(2)在FD上取一点H,使得FH=FE.
∵∠DEF=∠CEB=90°,∠DEC=∠DAB=75°,
∴∠BEF=105°,
∴∠FAB+∠FEB=180°,
∴∠AFE=180°-∠ABE=120°,
∴△HFE=60°,
∴△FHE是等边三角形,
∴∠HEF=∠AEB,
∴∠HEA=∠FEB,∵EH=EF,EA=EB,
∴△HEA≌△FEB,
∴AH=FB,
∴AF+FH=FB,∵FH=FE,
∴EF+FA=FB.
点评 本题考查平行四边形的性质、等边三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是发现△ABE是等边三角形,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

练习册系列答案
相关题目
6.下列运算可直接运用平方差公式的是( )
| A. | (a+b)(-a+b) | B. | (a+b)(-a-b) | C. | (a+b)(b+a) | D. | (a-b)(b-a) |
20.2016年深圳市生产总值同比增长9%,记作+9%,而尼日利亚国内生产总值同比下滑2.24%,应记作( )
| A. | 2.24% | B. | -2.24% | C. | 2.24 | D. | -2.24 |
1.下列所述图形中,既是中心对称图形,又是轴对称图形的是( )
| A. | 正三角形 | B. | 平行四边形 | C. | 矩形 | D. | 正五边形 |
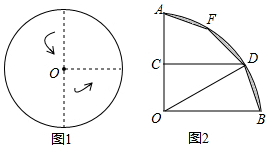 如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交$\widehat{AB}$于点D,点F是$\widehat{AB}$上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为36π-108.
如图1,将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB.已知OA=6,取OA的中点C,过点C作CD⊥OA交$\widehat{AB}$于点D,点F是$\widehat{AB}$上一点.若将扇形BOD沿OD翻折,点B恰好与点F重合,用剪刀沿着线段BD,DF,FA依次剪下,则剪下的纸片(形状同阴影图形)面积之和为36π-108.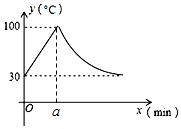 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图,
教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图,