题目内容
2.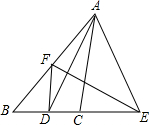 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF分别交AB,BC的延长线于点E,F,试说明:DF∥AC.
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF分别交AB,BC的延长线于点E,F,试说明:DF∥AC.
分析 先根据线段垂直平分线的性质得出AF=DF,由等边对等角得到∠FAD=∠FDA,再根据角平分线定义得出∠BAD=∠CAD,等量代换得出∠ADF=∠CAD,再根据内错角相等两直线平行即可证明DF∥AC.
解答 证明:∵EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠FDA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠ADF=∠CAD,
∴DF∥AC.
点评 本题考查了线段垂直平分线性质,三角形外角的性质,角平分线定义,平行线的判定等知识点的运用,难度适中,培养了学生综合运用性质进行推理的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
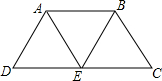 四边形ABCD中,DC∥AB,DC=2AB,E为DC的中点,连结AE、EB
四边形ABCD中,DC∥AB,DC=2AB,E为DC的中点,连结AE、EB