题目内容
10.一个n边形的内角和与它的外角和相等,求这个多边形的边数n的值是多少?分析 根据多边形的内角和公式(n-2)•180°与多边形的外角和定理列式进行计算即可得解.
解答 解:设多边形的边数为n,根据题意得
(n-2)•180°=360°,
解得n=4.
点评 本题考查了多边形的内角和公式与外角和定理,熟记公式与定理是解题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
5.若a<0,b>0,且|a|>|b|,则a与b的和用|a|、|b|表示为( )
| A. | |a|-|b| | B. | -(|a|-|b|) | C. | |a|+|b| | D. | -(|a|+|b|) |
2.已知x1、x2是一元二次方程x2-2x-8=0的两个实数根,则x1•x2等于( )
| A. | 2 | B. | -8 | C. | -2 | D. | 8 |
20.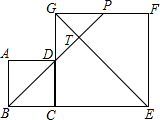 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )
 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
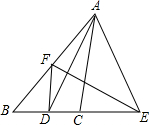 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF分别交AB,BC的延长线于点E,F,试说明:DF∥AC.
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF分别交AB,BC的延长线于点E,F,试说明:DF∥AC.
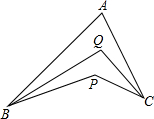 已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=$\frac{1}{2}$(α+β).(用α,β表示)
已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=$\frac{1}{2}$(α+β).(用α,β表示) 已知△ABC在平面直角坐标系中的位置如图所示
已知△ABC在平面直角坐标系中的位置如图所示