题目内容
10．三角形的三边是三个连续的奇数，最长边是2k+5（k为大于1的整数），则其它两边分别分别是2k+3和2k+1，猜想：这个三角形的最长边与最短边之和与第三边有何关系，试说明理由．分析 利用连续奇数相差2，表示出其它两条边即可；进一步计算最长边与最短边之和，得出结论即可．
解答 解：最长边是2k+5（k为大于1的整数），则其它两边分别2k+3，2k+1，
∵2k+5+2k+1=4k+6=2（2k+3），
∴这个三角形的最长边与最短边之和是第三边2倍．
故答案为：2k+3，2k+1．
点评 此题考查列代数式，掌握连续奇数的特征是解决问题的关键．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
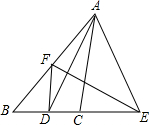如图，在△ABC中，AD是∠BAC的平分线，AD的垂直平分线EF分别交AB，BC的延长线于点E，F，试说明：DF∥AC．
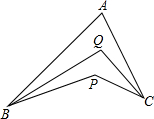已知如图，BQ平分∠ABP，CQ平分∠ACP，∠BAC=α，∠BPC=β，则∠BQC=$\frac{1}{2}$（α+β）．（用α，β表示）