题目内容
11.等腰三角形ABC内接于圆O,AB=AC,AB的垂直平分线MN与边AB交于点M,与AC所在的直线交于点N,若∠ANM=70°,则劣弧$\widehat{AC}$所对的圆心角的度数为160°或20°.分析 此题根据△ABC中∠A为锐角与钝角,分为两种情况解答,由线段垂直平分线的性质与等腰三角形的性质即可求得答案.
解答 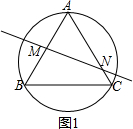 解:当∠A 为锐角时,如图1,
解:当∠A 为锐角时,如图1,
∵MN是AB的垂直平分线,
∴∠AMN=90°,
∵∠ANM=70°,
∴∠A=20°,
∵AB=AC,
∴∠B=80°,
∴劣弧$\widehat{AC}$所对的圆心角的度数为:160°;
当∠A为钝角时,如图2,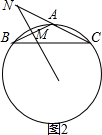
∵MN是AB的垂直平分线,
∴∠AMN=90°,
∵∠ANM=70°,
∴∠BAN=20°,
∴∠BAC=160°,
∵AB=AC,
∴∠B=10°,
∴劣弧$\widehat{AC}$所对的圆心角的度数为:20°,
故答案为:160°或20°.
点评 本题考查的是三角形的外接圆与外心,线段垂直平分线的性质以及等腰三角形的性质,此类题需要注意的是要分两种情况解答,考生在考虑问题时要全面.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
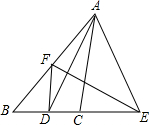 如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF分别交AB,BC的延长线于点E,F,试说明:DF∥AC.
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线EF分别交AB,BC的延长线于点E,F,试说明:DF∥AC.
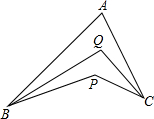 已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=$\frac{1}{2}$(α+β).(用α,β表示)
已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=$\frac{1}{2}$(α+β).(用α,β表示)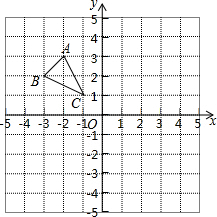 已知△ABC在平面直角坐标系中的位置如图所示
已知△ABC在平面直角坐标系中的位置如图所示