题目内容
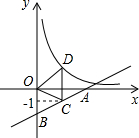 如图,直线y=
如图,直线y=| 1 |
| 2 |
| k |
| x |
| 7 |
| 2 |
考点:反比例函数与一次函数的交点问题
专题:
分析:根据点C在直线y=
x-2,可得点C的坐标,根据三角形的面积,可得DC的长,可得D点的坐标,根据待定系数法,可得答案.
| 1 |
| 2 |
解答:解;∵直线y=
x-2,点C在直线上,且点C的纵坐标为-1,
∴x=2,
∴点C(2,-1),
∵CD平行于y轴,
∴O到CD的距离是2,
设D(2,y),则DC=y+1
∵S△OCD=
×2×(y+1)=
,
∴y=
,
∴D(2,
)
∵点D在反比例函数y=
的图象上
∴k=xy=2×
=5,
故答案为:5.
| 1 |
| 2 |
∴x=2,
∴点C(2,-1),
∵CD平行于y轴,
∴O到CD的距离是2,
设D(2,y),则DC=y+1
∵S△OCD=
| 1 |
| 2 |
| 7 |
| 2 |
∴y=
| 5 |
| 2 |
∴D(2,
| 5 |
| 2 |
∵点D在反比例函数y=
| k |
| x |
∴k=xy=2×
| 5 |
| 2 |
故答案为:5.
点评:本题考查了反比例函数与一次函数的交点问题,利用三角形的面积公式,待定系数法求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
等式
=
成立的条件是( )
| ||
|
|
| A、0≤x<1 | B、x≥0 |
| C、x<1 | D、x≥0或x<1 |
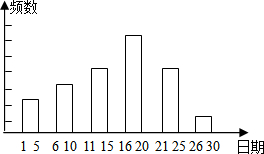 某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答:
某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答: 如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2
如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2 如图,点B在点A北偏东50°方向,点C在点B北偏西40°方向,BC=10m,则点C到直线AB的距离为
如图,点B在点A北偏东50°方向,点C在点B北偏西40°方向,BC=10m,则点C到直线AB的距离为 如图,⊙O与⊙O1内切于点A,⊙O的弦BC与⊙O1相切于点D,且BC∥O1O,BC=4,则图中阴影部分的面积为
如图,⊙O与⊙O1内切于点A,⊙O的弦BC与⊙O1相切于点D,且BC∥O1O,BC=4,则图中阴影部分的面积为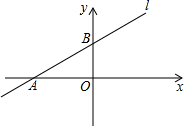 如图,直线l交x轴的负半轴于点A,交y轴的正半轴于点B,线段OA、OB的长分别是方程x2-14x+48=0(OA>OB)的两根的
如图,直线l交x轴的负半轴于点A,交y轴的正半轴于点B,线段OA、OB的长分别是方程x2-14x+48=0(OA>OB)的两根的