题目内容
 如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2
如图,在⊙O中,直径EF⊥CD,垂足为M,若CD=2| 5 |
考点:垂径定理,勾股定理
专题:
分析:连接OC,设⊙O的半径为R,则OC=R,OM=5-R,根据垂径定理求出CM,根据勾股定理得出方程,求出即可.
解答: 解:连接OC,设⊙O的半径为R,则OC=R,OM=5-R,
解:连接OC,设⊙O的半径为R,则OC=R,OM=5-R,
∵直径EF⊥CD,垂足为M,CD=2
,
∴CM=DM=
,
在Rt△OMC中,由勾股定理得:OC2=OM2+CM2,
R2=(5-R)2+(
)2,
解得R=3.
故答案为3.
 解:连接OC,设⊙O的半径为R,则OC=R,OM=5-R,
解:连接OC,设⊙O的半径为R,则OC=R,OM=5-R,∵直径EF⊥CD,垂足为M,CD=2
| 5 |
∴CM=DM=
| 5 |
在Rt△OMC中,由勾股定理得:OC2=OM2+CM2,
R2=(5-R)2+(
| 5 |
解得R=3.
故答案为3.
点评:本题考查了勾股定理,垂径定理的应用,用了方程思想,题目比较典型,难度适中.

练习册系列答案
相关题目
已知
是二元一次方程组
的解,则a-b的值为( )
|
|
| A、-1 | B、1 | C、2 | D、3 |
 在如图所示的网格纸上建立平面直角坐标系,在Rt△ABO中,∠OAB=90°,且点B的坐标为(2,3).
在如图所示的网格纸上建立平面直角坐标系,在Rt△ABO中,∠OAB=90°,且点B的坐标为(2,3). 全民健身是指不分男女老少,全面提高国民体质和健康水平,以青少年和儿童为重点,每年进行一次体质测定.小明和爷爷二人同时从家到健身馆,小明跑步,爷爷步行,小明到达健身馆后休息了5分钟,然后以练习竞走的方式迎接爷爷,速度为原来的一半,在途中与爷爷相遇,二人之间的距离y(m)与时间x(分)之间的关系如图,则小明家到健身馆的距离为
全民健身是指不分男女老少,全面提高国民体质和健康水平,以青少年和儿童为重点,每年进行一次体质测定.小明和爷爷二人同时从家到健身馆,小明跑步,爷爷步行,小明到达健身馆后休息了5分钟,然后以练习竞走的方式迎接爷爷,速度为原来的一半,在途中与爷爷相遇,二人之间的距离y(m)与时间x(分)之间的关系如图,则小明家到健身馆的距离为
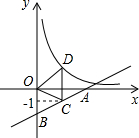 如图,直线y=
如图,直线y=