题目内容
 如图,⊙O与⊙O1内切于点A,⊙O的弦BC与⊙O1相切于点D,且BC∥O1O,BC=4,则图中阴影部分的面积为
如图,⊙O与⊙O1内切于点A,⊙O的弦BC与⊙O1相切于点D,且BC∥O1O,BC=4,则图中阴影部分的面积为考点:切线的性质,勾股定理,垂径定理
专题:计算题
分析:作OH⊥BC于H,连结O1D,OC,根据垂径定理得BH=CH=
BC=2,再根据切线的性质由BC与⊙O1相切于点D得O1D⊥BC,由于BC∥O1O,则O1D⊥OO1,易得四边形OHDO1为矩形,所以OH=O1D,在Rt△OCH中,根据勾股定理得OC2-OH2=CH2=4,即有OC2-O1D2=4,然后根据圆的面积公式得到S阴影部分=S大圆-S小圆=π(OC2-O1D2)=4π.
| 1 |
| 2 |
解答:解: 作OH⊥BC于H,连结O1D,OC,如图,
作OH⊥BC于H,连结O1D,OC,如图,
∵OH⊥BC,
∴BH=CH=
BC=
×4=2,
∵⊙O的弦BC与⊙O1相切于点D,
∴O1D⊥BC,
∵BC∥O1O,
∴O1D⊥OO1,
而OH⊥BC,
∴四边形OHDO1为矩形,
∴OH=O1D,
在Rt△OCH中,OC2-OH2=CH2=4,
∴OC2-O1D2=4,
∵S阴影部分=S大圆-S小圆
=π•OC2-π•O1D2
=π(OC2-O1D2)
=4π.
故答案为4π.
 作OH⊥BC于H,连结O1D,OC,如图,
作OH⊥BC于H,连结O1D,OC,如图,∵OH⊥BC,
∴BH=CH=
| 1 |
| 2 |
| 1 |
| 2 |
∵⊙O的弦BC与⊙O1相切于点D,
∴O1D⊥BC,
∵BC∥O1O,
∴O1D⊥OO1,
而OH⊥BC,
∴四边形OHDO1为矩形,
∴OH=O1D,
在Rt△OCH中,OC2-OH2=CH2=4,
∴OC2-O1D2=4,
∵S阴影部分=S大圆-S小圆
=π•OC2-π•O1D2
=π(OC2-O1D2)
=4π.
故答案为4π.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了勾股定理和垂径定理.

练习册系列答案
相关题目
分式方程
-1=
的解为( )
| 1 |
| x-2 |
| 1 |
| 2-x |
| A、x=4 | B、x=2 |
| C、x=0 | D、无解 |
已知
是二元一次方程组
的解,则a-b的值为( )
|
|
| A、-1 | B、1 | C、2 | D、3 |
 在如图所示的网格纸上建立平面直角坐标系,在Rt△ABO中,∠OAB=90°,且点B的坐标为(2,3).
在如图所示的网格纸上建立平面直角坐标系,在Rt△ABO中,∠OAB=90°,且点B的坐标为(2,3).
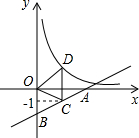 如图,直线y=
如图,直线y=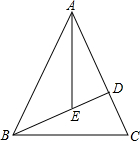 如图,在△ABC中,AB=AC=3,高BD=
如图,在△ABC中,AB=AC=3,高BD=