题目内容
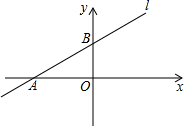 如图,直线l交x轴的负半轴于点A,交y轴的正半轴于点B,线段OA、OB的长分别是方程x2-14x+48=0(OA>OB)的两根的
如图,直线l交x轴的负半轴于点A,交y轴的正半轴于点B,线段OA、OB的长分别是方程x2-14x+48=0(OA>OB)的两根的| 1 |
| 3 |
(1)求点A、B的坐标;
(2)若点M在直线l上,且AM=
| 10 |
| 9 |
(3)若点P在射线AB上且BP=10,在x轴上是否存在点Q使以点B、P、Q为顶点的三角形是直角三角形?若存在请直接写出点Q的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)首先解x2-14x+48=0,即可求得点A与B的坐标;
(2)利用(1)中点的坐标,待定系数法即可求得直线l的解析式,设出点M的坐标,利用两点间的距离表示AM建立方程,解出方程求得坐标;
(3)因为点P在射线AB上且BP=10,所以点P在第一象限,设出坐标,利用两点间的距离求得BP,进一步得出P点坐标,再进一步分类探讨点Q的坐标即可.
(2)利用(1)中点的坐标,待定系数法即可求得直线l的解析式,设出点M的坐标,利用两点间的距离表示AM建立方程,解出方程求得坐标;
(3)因为点P在射线AB上且BP=10,所以点P在第一象限,设出坐标,利用两点间的距离求得BP,进一步得出P点坐标,再进一步分类探讨点Q的坐标即可.
解答:解:(1)x2-14x+48=0,
解得x1=6,x2=8,
∵OA>OB,
∴OA=8×
=
,OB=6×
=2,
∴点A坐标为(-
,0),点B坐标为(0,2).
(2)设直线l=kx+b,把点A、B代入得:
,
解得k=
,b=2,
∴l=
x+2,
∵点M在直线l上,设点M坐标为(x,
x+2),
∴AM=
=
,
整理得出(
x+
)2=
,
解得x=-
或x=-
,
则
x+2=
或
x+2=-
,
∴点M坐标为(-
,
)或(-
,-
),
设经过两点O、M的直线的解析式为y=kx,
代入M点得出y=-
x或y=
x;
(3)存在点Q使以点B、P、Q为顶点的三角形是直角三角形.
由题意设P为(x,
x+2)
则BP=
=10
解得x=8或x=-8,
∵P在射线AB上,
∴x=8,
则点P坐标为(8,8)
以点B、P、Q为顶点的三角形是直角三角形,
①当∠PBQ=90°,则经过B、Q两点的直线为y=-
x+2,求得点Q坐标为(
,0)
②当∠BPQ=90°,则经过P、Q两点的直线为y=-
x+
,求得点Q坐标为(14,0)
③当∠PQB=90°,设Q点坐标为(x,0),则由勾股定理BQ2+PQ2=PB2,得出x2+22+(x-8)2+82=102,
解得x=4,点Q坐标为(4,0)
综上所知点Q坐标为(
,0)或(14,0)或(4,0).
解得x1=6,x2=8,
∵OA>OB,
∴OA=8×
| 1 |
| 3 |
| 8 |
| 3 |
| 1 |
| 3 |
∴点A坐标为(-
| 8 |
| 3 |
(2)设直线l=kx+b,把点A、B代入得:
|
解得k=
| 3 |
| 4 |
∴l=
| 3 |
| 4 |
∵点M在直线l上,设点M坐标为(x,
| 3 |
| 4 |
∴AM=
(x+
|
| 10 |
| 9 |
整理得出(
| 5 |
| 4 |
| 10 |
| 3 |
| 100 |
| 81 |
解得x=-
| 16 |
| 9 |
| 32 |
| 9 |
则
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
∴点M坐标为(-
| 16 |
| 9 |
| 2 |
| 3 |
| 32 |
| 9 |
| 2 |
| 3 |
设经过两点O、M的直线的解析式为y=kx,
代入M点得出y=-
| 3 |
| 8 |
| 3 |
| 16 |
(3)存在点Q使以点B、P、Q为顶点的三角形是直角三角形.
由题意设P为(x,
| 3 |
| 4 |
则BP=
x2+(
|
解得x=8或x=-8,
∵P在射线AB上,
∴x=8,
则点P坐标为(8,8)
以点B、P、Q为顶点的三角形是直角三角形,
①当∠PBQ=90°,则经过B、Q两点的直线为y=-
| 4 |
| 3 |
| 3 |
| 2 |
②当∠BPQ=90°,则经过P、Q两点的直线为y=-
| 4 |
| 3 |
| 56 |
| 3 |
③当∠PQB=90°,设Q点坐标为(x,0),则由勾股定理BQ2+PQ2=PB2,得出x2+22+(x-8)2+82=102,
解得x=4,点Q坐标为(4,0)
综上所知点Q坐标为(
| 3 |
| 2 |
点评:此题考查一次函数的综合运用,两点间的距离计算方法,以及分类讨论思想的渗透,是一道比较难的题目.

练习册系列答案
相关题目
已知
是二元一次方程组
的解,则a-b的值为( )
|
|
| A、-1 | B、1 | C、2 | D、3 |
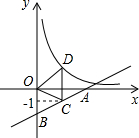 如图,直线y=
如图,直线y=