Question

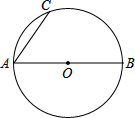如图，AB是⊙O的直径，AC是弦．
（1）请你按下面步骤画图（画图或作辅助线时先使用铅笔画出，确定后必须使用黑色字迹的签字笔描黑）；
第一步，过点A作∠BAC的角平分线，交⊙O于点D；第二步，过点D作AC的垂线，交AC的延长线于点E．
第三步，连接BD．
（2）求证：DE是⊙O的切线；
（3）若AD=5，AE=4，求⊙O的直径．

Answer 1

考点：切线的判定,作图—复杂作图

专题：

分析：（1）根据题意画出图形即可；
（2）连接OD，只要求出OD⊥DE，即可得出答案；
（3）求出△EAD∽△DAB，得出比例式，代入求出即可．

解答：（1）解：如图
；

（2）证明：连接OD，

∴∠ODA=∠DAO，
∵AD平分∠BAC，
∴∠CAD=∠BAD，
∴∠CAD=∠ADO，
∴OD∥AC，
∵DE⊥AC，
∴DE⊥OD，
∵OD为半径，
∴DE是⊙O的切线；

（3）解：∵AB为直径，DE⊥AC，
∴∠BDA=∠E=90°，
∵∠EAD=∠DAB，
∴△EAD∽△DAB，
∴

AE

AD

=

AD

AB

，
∴

4

5

=

5

AB

，
∴AB=

25

4

，
∴⊙O的直径是

25

4

．

点评：本题考查了切线的判定，圆周角定理，平行线的性质和判定，等腰三角形性质，相似三角形的性质和判定的应用，题目比较典型，是一定比较好的题目，难度适中．