题目内容
 如图,已知平行四边形ABCD,以AD、BC为边分别向外作等边△ADE和等边△BCF,求证:四边形DEBF是平行四边形.
如图,已知平行四边形ABCD,以AD、BC为边分别向外作等边△ADE和等边△BCF,求证:四边形DEBF是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:根据平行四边形的判定方法:两组对边相等的四边形是平行四边形即可证明四边形DEBF是平行四边形.
解答:证明:∵四边形ABCD是平行四边形,
∴AD=BC,DC=AB,∠DAB=∠DCB,
∵以AD、BC为边分别向外作等边△ADE和等边△BCF,
∴AD=DE=AE,BF=BC,
∴AE=CF,
∵∠EAB=∠DAB+∠DAE,∠DCF=∠DCB+∠BCF,
∴∠EAB=∠DCF,
在△EAB和△DCF中,
,
∴△EAB≌△DCF(SAS),
∴BE=FD,
∴四边形DEBF是平行四边形.
∴AD=BC,DC=AB,∠DAB=∠DCB,
∵以AD、BC为边分别向外作等边△ADE和等边△BCF,
∴AD=DE=AE,BF=BC,
∴AE=CF,
∵∠EAB=∠DAB+∠DAE,∠DCF=∠DCB+∠BCF,
∴∠EAB=∠DCF,
在△EAB和△DCF中,
|
∴△EAB≌△DCF(SAS),
∴BE=FD,
∴四边形DEBF是平行四边形.
点评:本题考查了平行四边形的判定和性质、全等三角形的判定和性质,解题的关键是熟记平行四边形的判定方法,并且灵活运用判定方法.

练习册系列答案
相关题目
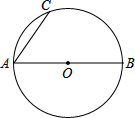 如图,AB是⊙O的直径,AC是弦.
如图,AB是⊙O的直径,AC是弦. 如图,△ABC中AB=13,BC=14,AC=15,BC边上高为AD,求△ABC的面积.
如图,△ABC中AB=13,BC=14,AC=15,BC边上高为AD,求△ABC的面积.