题目内容
1．某车间计划加工360个零件，由于技术上的改进，提高了工作效率，每天比原计划多加工20%，结果提前10天完成任务，求原计划每天能加工多少个零件？分析 关键描述语为：“提前10天完成任务”；等量关系为：原计划天数=实际生产天数+10．
解答 解：设原计划每天能加工x个零件，
可得：$\frac{360}{x}=\frac{360}{1.2x}+10$，
解得：x=6，
经检验x=6是原方程的解，
答：原计划每天能加工6个零件．
点评 本题考查分式方程的应用，分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．本题需注意应设较小的量为未知数．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．
如图，点A在以BC为直径的⊙O内，且AB=AC，以点A为圆心，AC长为半径作弧，得到扇形ABC，剪下扇形ABC围成一个圆锥（AB和AC重合），若∠BAC=120°，BC=2$\sqrt{3}$，则这个圆锥底面圆的半径是（ ）
如图，点A在以BC为直径的⊙O内，且AB=AC，以点A为圆心，AC长为半径作弧，得到扇形ABC，剪下扇形ABC围成一个圆锥（AB和AC重合），若∠BAC=120°，BC=2$\sqrt{3}$，则这个圆锥底面圆的半径是（ ）| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
如图，在?ABCD中，AB=3，BC=5，以点B的圆心，以任意长为半径作弧，分别交BA、BC于点P、Q，再分别以P、Q为圆心，以大于$\frac{1}{2}$PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为2．
9．下列计算正确的是（ ）
| A． | x2+3x2=4x4 | B． | x2y•2x3=2x4y | C． | （6x3y2）÷（3x）=2x2 | D． | （-3x）2=9x2 |
如图，从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件，另一个作为结论所组成的命题中，正确命题的个数为（ ）
6．从分别标有数-3，-2，-1，0，1，2，3的七张没有明显差别的卡片中，随机抽取一张，所抽卡片上的数的绝对值不小于2的概率是（ ）
| A． | $\frac{1}{7}$ | B． | $\frac{2}{7}$ | C． | $\frac{3}{7}$ | D． | $\frac{4}{7}$ |
10．
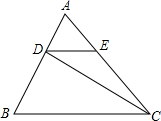如图，在△ABC中，DE∥BC，且S△ADE：S△CDE=1：3，则S△ADE：S△DBC等于（ ）
如图，在△ABC中，DE∥BC，且S△ADE：S△CDE=1：3，则S△ADE：S△DBC等于（ ）| A． | 1：5 | B． | 1：12 | C． | 1：8 | D． | 1：9 |
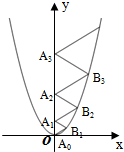二次函数y=$\frac{2}{3}$x2的图象如图所示，点A0位于坐标原点，A1，A2，A3，…，A2016在y轴的正半轴上，B1，B2，B3，…，B2016 在二次函数y=$\frac{2}{3}$x2第一象限的图象上，若△A0B1A1，△A1B2A2，△A2B3A3，…，△A2015B2016A2016都为等边三角形，则△A2015B2016A2016的边长=2016．