题目内容
3.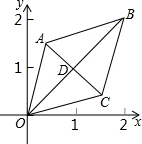 如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )
如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为( )| A. | (1,-1) | B. | (-1,-1) | C. | ($\sqrt{2}$,0) | D. | (0,-$\sqrt{2}$) |
分析 根据菱形的性质,可得D点坐标,根据旋转的性质,可得D点的坐标.
解答 解:菱形OABC的顶点O(0,0),B(2,2),得
D点坐标为(1,1).
每秒旋转45°,则第60秒时,得
45°×60=2700°,
2700°÷360=7.5周,
OD旋转了7周半,菱形的对角线交点D的坐标为(-1,-1),
故选:B.
点评 本题考查了旋转的性质,利用旋转的性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.在求3x的倒数的值时,嘉淇同学误将3x看成了8x,她求得的值比正确答案小5.依上述情形,所列关系式成立的是( )
| A. | $\frac{1}{3x}$=$\frac{1}{8x}$-5 | B. | $\frac{1}{3x}$=$\frac{1}{8x}$+5 | C. | $\frac{1}{3x}$=8x-5 | D. | $\frac{1}{3x}$=8x+5 |
11. 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
18.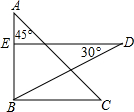 把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
 把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )| A. | 内部 | B. | 外部 | C. | 边上 | D. | 以上都有可能 |
8.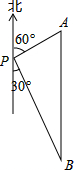 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
 如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )
如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为30海里的A处,轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则此时轮船所在位置B处与灯塔P之间的距离为( )| A. | 60海里 | B. | 45海里 | C. | 20$\sqrt{3}$海里 | D. | 30$\sqrt{3}$海里 |
15.面积为2的正方形的边长在( )
| A. | 0和1之间 | B. | 1和2之间 | C. | 2和3之间 | D. | 3和4之间 |
 如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.
如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE. 如图,在?ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于$\frac{1}{2}$PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为2.
如图,在?ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于$\frac{1}{2}$PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为2.