题目内容
2.某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是100.
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
分析 (1)根据10~15吨部分的用户数和百分比进行计算;(2)先根据频数分布直方图中的数据,求得“15吨~20吨”部分的用户数,再画图,最后根据该部分的用户数计算圆心角的度数;(3)根据用水25吨以内的用户数的占比,求得该地区6万用户中用水全部享受基本价格的户数.
解答 解:(1)∵10÷10%=100(户)
∴样本容量是100;
(2)用水15~20吨的户数:100-10-36-24-8=22(户)
∴补充图如下: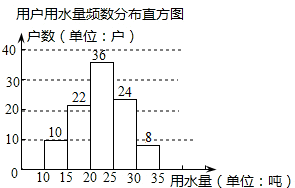
“15吨~20吨”部分的圆心角的度数=360°×$\frac{22}{100}$=79.2°
答:扇形图中“15吨~20吨”部分的圆心角的度数为79.2°.
(3)6×$\frac{10+22+36}{100}$=4.08(万户)
答:该地区6万用户中约有4.08万户的用水全部享受基本价格.
点评 本题主要考查了频数分布直方图和扇形统计图,解决问题的关键是在图中获取相关的数据进行计算求解.注意:扇形圆心角的度数=360°×该部分在总数中的百分比,扇形统计图可以更清楚的了解各部分数量同总数之间的关系.此外,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
13.在求3x的倒数的值时,嘉淇同学误将3x看成了8x,她求得的值比正确答案小5.依上述情形,所列关系式成立的是( )
| A. | $\frac{1}{3x}$=$\frac{1}{8x}$-5 | B. | $\frac{1}{3x}$=$\frac{1}{8x}$+5 | C. | $\frac{1}{3x}$=8x-5 | D. | $\frac{1}{3x}$=8x+5 |
17. 一个几何体的三视图如图所示,则该几何体的表面积为( )
一个几何体的三视图如图所示,则该几何体的表面积为( )
 一个几何体的三视图如图所示,则该几何体的表面积为( )
一个几何体的三视图如图所示,则该几何体的表面积为( )| A. | 4π | B. | 3π | C. | 2π+4 | D. | 3π+4 |
7.下列事件中,是必然事件的是( )
| A. | 三条线段可以组成一个三角形 | B. | 400人中有两个人的生日在同一天 | ||
| C. | 早上的太阳从西方升起 | D. | 打开电视机,它正在播放动画片 |
11. 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
 如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )
如图,点A在以BC为直径的⊙O内,且AB=AC,以点A为圆心,AC长为半径作弧,得到扇形ABC,剪下扇形ABC围成一个圆锥(AB和AC重合),若∠BAC=120°,BC=2$\sqrt{3}$,则这个圆锥底面圆的半径是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
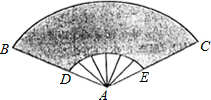 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,AB的长为30cm,扇面贴纸部分BD的长为20cm.则贴纸部分的面积为$\frac{1000}{3}$πcm2(结果保留π).
如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,AB的长为30cm,扇面贴纸部分BD的长为20cm.则贴纸部分的面积为$\frac{1000}{3}$πcm2(结果保留π). 如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.
如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE. 如图,在?ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于$\frac{1}{2}$PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为2.
如图,在?ABCD中,AB=3,BC=5,以点B的圆心,以任意长为半径作弧,分别交BA、BC于点P、Q,再分别以P、Q为圆心,以大于$\frac{1}{2}$PQ的长为半径作弧,两弧在∠ABC内交于点M,连接BM并延长交AD于点E,则DE的长为2.