题目内容
11.阅读下列材料,完成相应学习任务:四点共圆的条件
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?小明经过实践探究发现:过对角互补的四边形的四个顶点能作一个圆,下面是小明运用反证法证明上述命题的过程:
已知:在四边形ABCD中,∠B+∠D=180°.
求证:过点A、B、C、D可作一个圆.
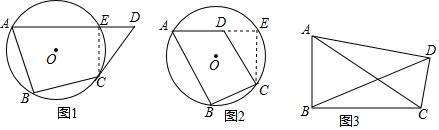
证明:如图(1),假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆外,设AD与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠D=180°,所以∠AEC=∠D,而∠AEC是△CED的外角,∠AEC>∠D,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
如图(2)假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆内,设AD的延长线与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠ADCA=180°,所以∠AEC=∠ADC,而∠ADC是△CED的外角,∠ADC>∠AEC,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
因此得到四点共圆的条件:过对角互补的四边形的四个顶点能作一个圆.
学习任务:
(1)材料中划线部分结论的依据是圆的内接四边形对角互补.
(2)证明过程中主要体现了下列哪种数学思想:D(填字母代号即可)
A、函数思想 B、方程思想 C、数形结合思想 D、分类讨论思想
(3)如图(3),在四边形ABCD中,∠ABC=∠ADC=90°,∠CAD=16°.AD=BD,则求∠ADB的大小.
分析 (1)材料中划线部分结论的依据圆的内接四边形对角互补,
(2)证明过程中分点D在圆外或圆内两种情形讨论,主要体现了分类讨论的数学思想.
(3)利用“对角互补的四边形的四个顶点能作一个圆”这个结论,结合直径的性质以及等腰三角形的性质,即可解决问题.
解答 解:(1)材料中划线部分结论的依据圆的内接四边形对角互补,
故答案为材料中划线部分结论的依据
(2)证明过程中主要体现了分类讨论的数学思想,分点D在圆外或圆内两种情形讨论.
故答案为D;
(3)解:∵∠ABC+∠ADC=180°,
∴过四边形ABCD的四个顶点能作一个圆(如图所示),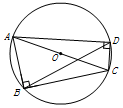
∴∠CBD=∠CAD=16°,
∴∠ABD=74°,
又∵AD=BD,
∴∠BAD=∠ABD=74°,
∴∠ADB=32°.
点评 本题考查圆综合题、推导了对角互补的四边形的四个顶点能作一个圆,解题的关键是利用结论解决问题,属于中考创新题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.如图所示,是由一些相同的小正方体搭成的几何体的三视图,则组成该几何体的小正方体的个数为( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则$\widehat{AC}$的长为2π.
如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为4,∠B=135°,则$\widehat{AC}$的长为2π.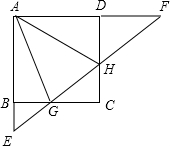 如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.
如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.