题目内容
6．阅读下面的问题，然后回答，分解因式：x2+2x-3，
解：原式
=x2+2x+1-1-3
=（x2+2x+1）-4
=（x+1）2-4
=（x+1+2）（x+1-2）
=（x+3）（x-1）
上述因式分解的方法称为配方法．请体会配方法的特点，用配方法分解因式：
（1）x2-4x+3
（2）4x2+12x-7．
分析 根据题意给出的方法即可求出答案．
解答 解：（1）x2-4x+3
=x2-4x+4-4+3
=（x-2）2-1
=（x-2+1）（x-2-1）
=（x-1）（x-3）
（2）4x2+12x-7
=4x2+12x+9-9-7
=（2x+3）2-16
=（2x+3+4）（2x+3-4）
=（2x+7）（2x-1）
点评 本题考查因式分解，涉及完全平方公式，平方差公式．
练习册系列答案
相关题目
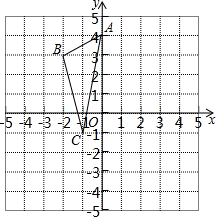如图，网格中每个小正方形的边长均为1，已知三角形ABC及三角形外一点D，平移三角形ABC使点A（0，4）移动到点D（3，2），得到三角形DEF，B（-2，3）的对应点为E，C（-1，-1）对应点F．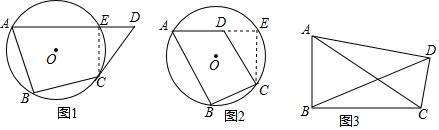
如图，若∠DAE=∠E，∠B=∠D，那么AB∥DC吗？请在下面的解答过程中填空或在括号内填写理由．