题目内容
8. 如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件∠A=∠D使得△ABC≌△DEF.
如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件∠A=∠D使得△ABC≌△DEF.
分析 根据全等三角形的判定定理填空.
解答  解:添加∠A=∠D.理由如下:
解:添加∠A=∠D.理由如下:
∵FB=CE,
∴BC=EF.
又∵AC∥DF,
∴∠ACB=∠DFE.
∴在△ABC与△DEF中,$\left\{\begin{array}{l}{∠A=∠D}\\{∠ACB=∠DFE}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(AAS).
故答案是:∠A=∠D.
点评 本题主要考查对全等三角形的判定,平行线的性质等知识点的理解和掌握,熟练地运用全等三角形的判定定理进行证明是解此题的关键,是一个开放型的题目,比较典型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.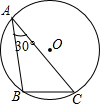 如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧$\widehat{BC}$的长等于( )
如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧$\widehat{BC}$的长等于( )
 如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧$\widehat{BC}$的长等于( )
如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧$\widehat{BC}$的长等于( )| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{2\sqrt{3}π}{3}$ | D. | $\frac{\sqrt{3}π}{3}$ |
3. 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( )
 如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=15°,半径为2,则弦CD的长为( )| A. | 2 | B. | -1 | C. | $\sqrt{2}$ | D. | 4 |
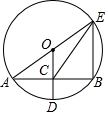 如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( )
如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( )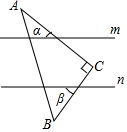 如图,直角三角板ABC的直角顶点C在两平行直线m,n之间,两直角边BC、AC与两直线m,n相交所形成的锐角分别为α、β,则α+β=90°.
如图,直角三角板ABC的直角顶点C在两平行直线m,n之间,两直角边BC、AC与两直线m,n相交所形成的锐角分别为α、β,则α+β=90°.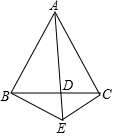 如图,在△ABC中,AB=AC,AD平分∠BAC,E是AD的延长线上任意一点,连接BE,CE.则四边形ABEC是轴对称图形吗?请简单说明理由.
如图,在△ABC中,AB=AC,AD平分∠BAC,E是AD的延长线上任意一点,连接BE,CE.则四边形ABEC是轴对称图形吗?请简单说明理由.