题目内容
16.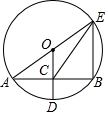 如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( )
如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为( )| A. | 12 | B. | 15 | C. | 16 | D. | 18 |
分析 先根据垂径定理求出AC的长,再设OA=r,则OC=r-2,在Rt△AOC中利用勾股定理求出r的值,再求出BE的长,利用三角形的面积公式即可得出结论.
解答 解:∵⊙O的半径OD垂直于弦AB,垂足为点C,AB=8,
∴AC=BC=$\frac{1}{2}$AB=4.
设OA=r,则OC=r-2,
在Rt△AOC中,
∵AC2+OC2=OA2,即42+(r-2)2=r2,解得r=5,
∴AE=10,
∴BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴△BCE的面积=$\frac{1}{2}$BC•BE=$\frac{1}{2}$×4×6=12.
故选A.
点评 本题考查的是圆周角定理,熟知直径所对的圆周角是直角是解答此题的关键.

练习册系列答案
相关题目
7.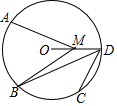 如图,A,B,C,D是⊙O上的四个点,B是$\widehat{AC}$的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
如图,A,B,C,D是⊙O上的四个点,B是$\widehat{AC}$的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
 如图,A,B,C,D是⊙O上的四个点,B是$\widehat{AC}$的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )
如图,A,B,C,D是⊙O上的四个点,B是$\widehat{AC}$的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是( )| A. | 45° | B. | 60° | C. | 75° | D. | 85° |
11.解分式方程$\frac{1}{x-1}$-2=$\frac{3}{1-x}$,去分母得( )
| A. | 1-2(x-1)=-3 | B. | 1-2(x-1)=3 | C. | 1-2x-2=-3 | D. | 1-2x+2=3 |
1.下列运算结果正确的是( )
| A. | 3a-a=2 | B. | (a-b)2=a2-b2 | C. | 6ab2÷(-2ab)=-3b | D. | a(a+b)=a2+b |
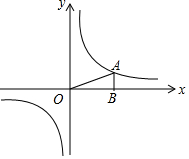 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2. 如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件∠A=∠D使得△ABC≌△DEF.
如图,点B、F、C、E在一条直线上,已知FB=CE,AC∥DF,请你添加一个适当的条件∠A=∠D使得△ABC≌△DEF. 如图是由24个边长为1的小正方形组成的6×4网格,此时小正方形的顶点称为格点,顶点在格点上的三角形称为格点三角形,已知△ABC中,AB=2,AC=$\sqrt{5}$,BC=$\sqrt{13}$.
如图是由24个边长为1的小正方形组成的6×4网格,此时小正方形的顶点称为格点,顶点在格点上的三角形称为格点三角形,已知△ABC中,AB=2,AC=$\sqrt{5}$,BC=$\sqrt{13}$.