题目内容
5.等边三角形的边长为2,则该三角形的高为$\sqrt{3}$.分析 作出一边上的高,利用勾股定理和等边三角形的性质可求得高.
解答  解:如图,△ABC为等边三角形,过A作AD⊥BC,交BC于点D,
解:如图,△ABC为等边三角形,过A作AD⊥BC,交BC于点D,
则BD=$\frac{1}{2}$AB=1,AB=2,
在Rt△ABD中,由勾股定理可得:AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题主要考查等边三角形的性质,掌握等边三角形“三线合一”的性质是解题的关键.

练习册系列答案
相关题目
20.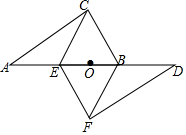 如图,在以AB为斜边的Rt△ABC中,AC=8,BC=6,点O为AB上一点,将△ABC绕点O旋转180°得到△DEF,连接EF、BF.若四边形CEFB为菱形,则AE的长为( )
如图,在以AB为斜边的Rt△ABC中,AC=8,BC=6,点O为AB上一点,将△ABC绕点O旋转180°得到△DEF,连接EF、BF.若四边形CEFB为菱形,则AE的长为( )
 如图,在以AB为斜边的Rt△ABC中,AC=8,BC=6,点O为AB上一点,将△ABC绕点O旋转180°得到△DEF,连接EF、BF.若四边形CEFB为菱形,则AE的长为( )
如图,在以AB为斜边的Rt△ABC中,AC=8,BC=6,点O为AB上一点,将△ABC绕点O旋转180°得到△DEF,连接EF、BF.若四边形CEFB为菱形,则AE的长为( )| A. | 2.4 | B. | 2.8 | C. | 3.6 | D. | 4.8 |
17.下列说法中正确的是( )
| A. | 3.14159是一个无理数 | B. | $\sqrt{0.25}$=±0.5 | ||
| C. | 若a为实数,则a2≥0 | D. | 16的平方根是4 |
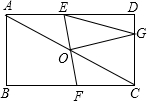 如图,矩形ABCD中,对角线AC的中点为O,过O作直线EF交AD于E,交BC于F.
如图,矩形ABCD中,对角线AC的中点为O,过O作直线EF交AD于E,交BC于F.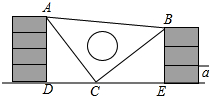 课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图所示.
课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图所示. 写出推理理由:
写出推理理由: