题目内容
20.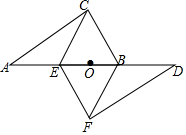 如图,在以AB为斜边的Rt△ABC中,AC=8,BC=6,点O为AB上一点,将△ABC绕点O旋转180°得到△DEF,连接EF、BF.若四边形CEFB为菱形,则AE的长为( )
如图,在以AB为斜边的Rt△ABC中,AC=8,BC=6,点O为AB上一点,将△ABC绕点O旋转180°得到△DEF,连接EF、BF.若四边形CEFB为菱形,则AE的长为( )| A. | 2.4 | B. | 2.8 | C. | 3.6 | D. | 4.8 |
分析 连接CF.由菱形的对角线互相平分以及旋转的性质可知O为为BE与CF的交点,从而可得到CO⊥BE,先求得AB的长,然后利用面积法可求得OC的长,在Rt△OBC中,依据勾股定理可求得OB的长,从而得到BE的长,最后由AE=AB-BE求即即可.
解答 解:如图所示:连接CF.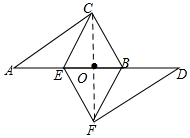
∵四边形BCEF为菱形,
∴BE⊥CF且EB与CF相互平分.
又∵由旋转的性质可知OE=OB,
∴点O为BE与CF的交点.
∴CO⊥BE.
∵BC=6,AC=8,∠ACB=90°,
∴AB=10.
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CO,
∴OC=$\frac{AC•BC}{AB}$=4.8.
在Rt△OBC中,依据勾股定理可知OB=$\sqrt{C{B}^{2}-O{C}^{2}}$=3.6.
∴BE=7.2.
∴AE=AB-BE=10-7.2=2.8.
故选:B.
点评 本题主要考查的是菱形的性质、旋转的性质、勾股定理的应用,证得点O为BE与CF的交点是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
15.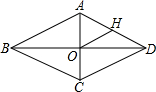 如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
 如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |