题目内容
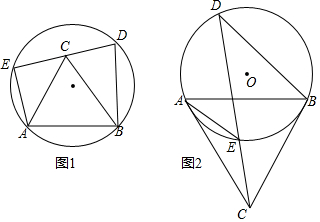
19.定义:既有外接圆,又有内切圆的凸多边形叫做双圆多边形.如图1,⊙O1是△ABC外接圆,⊙O2是△ABC的内切圆,则△ABC就是双圆三角形.(1)请写出一个双圆四边形的名你正方形;
(2)如图2,已知四边形ABCD是双圆四边形,其内切圆与四条边相切于点E,F,G,H,且EG是内切圆的直径,交弦FH于点P,连接EF,FG.
①当∠FGE=40°时,求∠BFE的度数;
②求证:HF⊥GE.
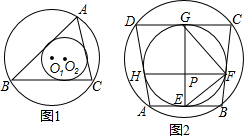
分析 (1)正方形既有外接圆,又有内切圆,所以正方形是双圆四边形;
(2)①如图2中,作直径FM,连接EM,首先证明∠EMF=∠EFB,于∠EMF=∠EGF,可得∠EFB=∠EGF=40°.
②如图3中,连接HG.首先证明∠DGH+∠EFB=90°,由①可知,∠EFB=∠EGF,∠DGH=∠HFG,即可推出∠EGF+∠HFG=90°,由此即可证明.
解答 解:(1)正方形既有外接圆,又有内切圆,所以正方形是双圆四边形,
故答案为正方形.
(2)①如图2中,作直径FM,连接EM,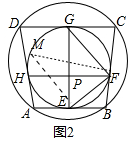
∵FM是直径,
∴∠MEF=90°,
∴∠EMF+∠MFE=90°,
∵BF是切线,
∴MF⊥BF,
∴∠MFB=90°,
∴∠MFE+∠EFB=90°,
∴∠EMF=∠EFB,
∵∠EMF=∠EGF,
∴∠EFB=∠EGF=40°.
②如图3中,连接HG.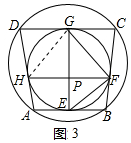
∵四边形ABCD是圆内接四边形,
∴∠D+∠B=180°,
∵H、G、F、E是切点,
∴DG=DH,BF=BE,
∴∠DHG=∠DGH,∠BEF=∠BFE,
∴∠D+2∠DGH=180°,∠B+2∠EFB=180°,
∴2∠DGH+2∠EFB=180°,
∴∠DGH+∠EFB=90°,
由①可知,∠EFB=∠EGF,∠DGH=∠HFG,
∴∠EGF+∠HFG=90°,
∴∠GPE=90°,
∴HF⊥GE.
点评 本题考查圆综合题、直径的性质、圆周角定理、切线长定理,圆内接四边形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,属于中考压轴题.

练习册系列答案
相关题目
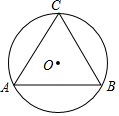 如图,⊙O是正△ABC的外接圆,$\widehat{AB}$的长度为$\frac{4}{3}$π,求△ABC的边长.
如图,⊙O是正△ABC的外接圆,$\widehat{AB}$的长度为$\frac{4}{3}$π,求△ABC的边长.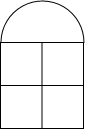 如图,是一扇窗户的设计图,它由四个小正方形及一个半圆组成,已知半圆的半径为a米.(结果保留π)
如图,是一扇窗户的设计图,它由四个小正方形及一个半圆组成,已知半圆的半径为a米.(结果保留π)