题目内容
8.(1)计算:$\sqrt{12}$-|-5|+3tan30°-($\frac{1}{2016}$)0;(2)解不等式$\frac{2}{3}$(x-1)≤x+1,并把它的解集在数轴上表示出来.
分析 (1)本题涉及二次根式化简、绝对值、特殊角的三角函数值、零指数幂4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)先去括号,再移项、合并同类项、最后系数化为1即可,再在数轴上把解集表示出来.
解答 解:(1)$\sqrt{12}$-|-5|+3tan30°-($\frac{1}{2016}$)0
=2$\sqrt{3}$-5+3×$\frac{\sqrt{3}}{3}$-1
=2$\sqrt{3}$-5+$\sqrt{3}$-1
=3$\sqrt{3}$-6;
(2)$\frac{2}{3}$(x-1)≤x+1,
$\frac{2}{3}$x-$\frac{2}{3}$≤x+1,
$\frac{2}{3}$x-x≤1+$\frac{2}{3}$,
-$\frac{1}{3}$x≤$\frac{5}{3}$,
x≥-5,
把解集画在数轴上为:
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握二次根式化简、绝对值、特殊角的三角函数值、零指数幂等考点的运算.同时考查了解一元一次不等式以及在数轴上表示不等式的解集,是基础知识要熟练掌握.

练习册系列答案
相关题目
18.已知反比例函数y=$\frac{1}{x}$,下列结论中不正确的是( )
| A. | 图象经过点(-$\frac{1}{2}$,-2) | B. | 图象位于第一、三象限 | ||
| C. | y随x的增大而减小 | D. | 当1<x<3时,y的取值范围是$\frac{1}{3}$<y<1 |
16.将分式方程$\frac{x}{x-3}=2-\frac{3}{3-x}$去分母得( )
| A. | x=2+3 | B. | x=2(x-3)+3 | C. | x=2(x-3)+3(x-3) | D. | x=2(x-3)-3 |
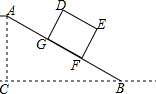 如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为2$\sqrt{5}$m.(结果保留根号)
如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为2$\sqrt{5}$m.(结果保留根号) 如图所示,正比例函数与反比例函数的图象相交于A、B两点,过点A作AC∥y轴交x轴于点C,过点D作DM∥x轴交双曲线y=$\frac{k}{x}$于点E,交直线AC于点M(4,2),得到四边形OAME的面积为4.
如图所示,正比例函数与反比例函数的图象相交于A、B两点,过点A作AC∥y轴交x轴于点C,过点D作DM∥x轴交双曲线y=$\frac{k}{x}$于点E,交直线AC于点M(4,2),得到四边形OAME的面积为4. 如图,直线l1∥l2,∠2=40°,则∠1+∠3+∠4=220°.
如图,直线l1∥l2,∠2=40°,则∠1+∠3+∠4=220°.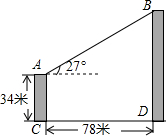 如图,甲、乙两栋大楼相距78米,一测量人员从甲楼AC的顶部看乙楼BD的顶部其仰角为27°.如果甲楼的高为34米,求乙楼的高度是多少米?(结果精确到0.1米)
如图,甲、乙两栋大楼相距78米,一测量人员从甲楼AC的顶部看乙楼BD的顶部其仰角为27°.如果甲楼的高为34米,求乙楼的高度是多少米?(结果精确到0.1米) (1)设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号
(1)设二次函数y=ax2+bx+c(a≠0)图象如图所示,经过点(-1,0),试判断a、b、c、a+b+c、a-b+c、b2-4ac的符号