题目内容
16.已知:|x-y-3|+(a+b+4)2=0,求代数式$\frac{(x-y)^{2}-3(y-x)}{2a+2b-(a+b)^{3}}$的值.分析 利用非负数的性质得出x-y,a+b的值,然后再整体代入即可.
解答 解:∵|x-y-3|+(a+b+4)2=0,
∴x-y-3=0,a+b+4=0,
解得:x-y=3,a+b=-4,
∴原式=$\frac{{(x-y)}^{2}-3(y-x)}{2(a+b){-(a+b)}^{3}}$=$\frac{{3}^{2}-3×(-3)}{2×(-4){-(-4)}^{3}}$=$\frac{9}{28}$.
点评 本题主要考查了非负数的性质,利用非负数的性质解得x-y,a+b的值,然后再整体代入是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
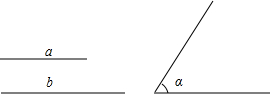 如图,已知:线段a,b和∠α.求作:△ABC,使∠BAC=∠α,高线AD=a,角平分线AE=b.
如图,已知:线段a,b和∠α.求作:△ABC,使∠BAC=∠α,高线AD=a,角平分线AE=b. 如图,△ABC中,D、E、F为BC、AD、BE的中点,若△CEF的面积是3,则△ABC的面积是12.
如图,△ABC中,D、E、F为BC、AD、BE的中点,若△CEF的面积是3,则△ABC的面积是12. 如图,一块四边形农田内有一条折路MPN,现欲将折路改直而道路两边的农田面积不变,应如何划线?
如图,一块四边形农田内有一条折路MPN,现欲将折路改直而道路两边的农田面积不变,应如何划线?