题目内容
10.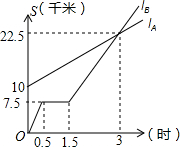 如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)走了一段路后,自行车因故障,进行修理,所用的时间是1小时.
(2)B出发后3小时与A相遇
(3)修理后的自行车速度是多少?A步行速度是多少?
(4)若B的自行车不发生故障,保持出发时的速度前进,几小时与A相遇?相遇点离B的出发点几千米?
(5)求出A行走的路程S与时间t的函数关系式.
分析 (1)根据函数图象可以直接得到走了一段路后,自行车因故障,进行修理,所用的时间;
(2)根据图象可以得到B出发几小时与A相遇;
(3)根据函数图象中的数据可以分别求得修理后的自行车速度和A步行速度;
(4)根据图象中的数据可以得到B出发时的速度,然后根据题意可知当A和B相遇时,他们走的总路程相等,从而可以求得相遇时的时间以及此时相遇点离B的距离;
(5)根据图象中的数据可以求得A行走的路程S与时间t的函数关系式.
解答 解:(1)由图象可得,
走了一段路后,自行车因故障,进行修理,所用的时间是:1.5-0.5=1(小时),
故答案为:1;
(2)由图象可得,
B出发3小时与A相遇,
故答案为:3;
(3)由图象可得,
修理后的自相车的速度为:(22.5-7.5)÷(3-1.5)=10千米/时,
A步行的速度为:(22.5-10)÷3=$\frac{25}{6}$千米/时;
(4)由图象可得,
B出发时的速度为:7.5÷0.5=15千米/时,
设若B的自行车不发生故障,保持出发时的速度前进,x小时与A相遇,
15x=10+$\frac{25x}{6}$,
解得,x=$\frac{12}{13}$,
∴15x=15×$\frac{12}{13}=\frac{180}{13}$,
即若B的自行车不发生故障,保持出发时的速度前进,$\frac{12}{13}$小时与A相遇,相遇点离B的出发点$\frac{180}{13}$千米;
(5)设A行走的路程S与时间t的函数关系式为:S=kt+b,
$\left\{\begin{array}{l}{b=10}\\{3k+b=22.5}\end{array}\right.$,得$\left\{\begin{array}{l}{k=\frac{25}{6}}\\{b=10}\end{array}\right.$,
即A行走的路程S与时间t的函数关系式是S=$\frac{25}{6}t+10$.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案| A. | 2x+4 | B. | 7 | C. | 5 | D. | 3 |
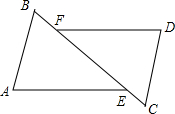 如图,AB=DC,BF=CE,需要补充一个条件,就能使△ABE≌△DCF,小明给出了四个答案::①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )
如图,AB=DC,BF=CE,需要补充一个条件,就能使△ABE≌△DCF,小明给出了四个答案::①AE=DF;②AE∥DF;③AB∥DC;④∠A=∠D,其中正确的是( )| A. | ①③ | B. | ①② | C. | ①②③ | D. | ①②③④ |
| A. | 6 | B. | 0 | C. | -6 | D. | -3 |
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |