题目内容

6．有一块长方形铁皮，长100cm，宽50cm，在它的四周各切去一个同样的正方形，然后将四周突出部分折起，就能制作一个无盖方盒．如果要制作的无盖方盒的底面积为3600cm2，设铁皮各角应切去的正方形边长为xcm，则下面所列方程正确的是（　　）
A．4x2=3600B．100×50-4x2=3600
C．（100-x）（50-x）=3600D．（100-2x）（50-2x）=3600

分析 易得底面积的长=原来的长-2×切去的正方形的边长，宽=原来的宽-2×切去的正方形的边长，根据长×宽=3600列方程即可．

解答 解：设切去的小正方形的边长为x．
根据题意得（100-2x）（50-2x）=3600．
故选D．

点评 考查一元二次方程的应用；得到无盖方盒的底面积的边长是解决本题的突破点．

练习册系列答案
相关题目
16．如果一个自然数能表示为两个自然数的平方差，那么称这个自然数为智慧数，例如：16=52-32，16就是一个智慧数，小明和小王对自然数中的智慧数进行了如下的探索：
小明的方法是一个一个找出来的：
0=02-02，1=12-02，3=22-12，
4=22-02，5=32-22，7=42-32，
8=32-12，9=52-42，11=62-52，…
小王认为小明的方法太麻烦，他想到：
设k是自然数，由于（k+1）2-k2=（k+1+k）（k+1-k）=2k+1．
所以，自然数中所有奇数都是智慧数．
问题：
（1）根据上述方法，自然数中第12个智慧数是15；
（2）他们发现0，4，8是智慧数，由此猜测4k（k≥3且k为正整数）都是智慧数，请你参考小王的办法证明4k（k≥3且k为正整数）都是智慧数；
（3）他们还发现2，6，10都不是智慧数，由此猜测4k+2（k为自然数）都不是智慧数，请利用所学的知识判断26是否是智慧数，并说明理由．
17．用代入法解方程组：$\left\{\begin{array}{l}{3x-y=7，①}\\{5x+2y=8②}\end{array}\right.$．
小明是这样解的：解：由①，得y=3x-7，③第一步
把③代人①，得3x-（3x-7）=7，第二步
即7=7．第三步
所以此方程组无解．第四步
你认为他的解法有误吗？若有误，错在第第二步步，请写出正确的解法．
14．已知关于x的不等式组$\left\{\begin{array}{l}{x＞a}\\{x＞1}\end{array}\right.$的解集为x＞1，则a的取值范围是a≤1．
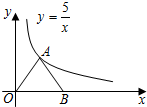1．已知反比例函数$y=\frac{5}{x}$在第一象限的图象如图所示，点A在其图象上，点B为x轴正半轴上一点，连接AO、AB，且AO=AB，则S△AOB=5．
11．已知正方形ABCD中，点E在边CD上，DE=3，EC=1．点F是正方形边上一点，且BF=AE，则FC=$\sqrt{17}$或3．
18．不等式组$\left\{\begin{array}{l}3x+5≥-1\\ 3-x＞\frac{1}{2}x\end{array}\right.$的解集为-2≤x＜2．
15．二次函数y=$\frac{2}{3}$x2-$\frac{\sqrt{2}}{3}$x+1的最小值是$\frac{11}{12}$．
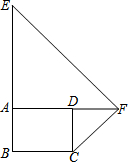13．已知，E，F在矩形ABCD的边BA，AD延长线上．若EB=EF=8，CB=CF=6，求矩形ABCD的面积是$\frac{864}{25}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网