题目内容
13.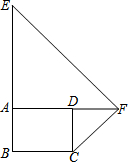 已知,E,F在矩形ABCD的边BA,AD延长线上.若EB=EF=8,CB=CF=6,求矩形ABCD的面积是$\frac{864}{25}$.
已知,E,F在矩形ABCD的边BA,AD延长线上.若EB=EF=8,CB=CF=6,求矩形ABCD的面积是$\frac{864}{25}$.
分析 由矩形的性质得出AD=BC=6,AB=CD,∠EAF=∠CDF=90°,设AB=CD=x,则AE=BE-AB=8-x,由勾股定理得出AF=$\sqrt{16x-{x}^{2}}$,因此DF=AF-AD=$\sqrt{16x-{x}^{2}}$-6,由勾股定理得出方程,解方程求出AB,即可得出矩形的面积.
解答 解:∵四边形ABCD是矩形,
∴AD=BC=6,AB=CD,∠BAD=∠ADC=90°,
∴∠EAF=∠CDF=90°,
设AB=CD=x,则AE=BE-AB=8-x,
∴AF=$\sqrt{E{F}^{2}-A{E}^{2}}$=$\sqrt{{8}^{2}-(8-x)^{2}}$=$\sqrt{16x-{x}^{2}}$,
∴DF=AF-AD=$\sqrt{16x-{x}^{2}}$-6,
∵DF2=CF2-CD2,
∴($\sqrt{16x-{x}^{2}}$-6)2+x2=62,
解得:x=$\frac{144}{25}$,或x=0(不合题意,舍去),
∴AB=$\frac{144}{25}$,
∴矩形ABCD的面积=BC•AD=6×$\frac{144}{25}$=$\frac{864}{25}$;
故答案为:$\frac{864}{25}$.
点评 本题考查了矩形的性质、勾股定理;熟练掌握矩形的性质,由勾股定理得出方程是解决问题的突破口.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.有一块长方形铁皮,长100cm,宽50cm,在它的四周各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3600cm2,设铁皮各角应切去的正方形边长为xcm,则下面所列方程正确的是( )
| A. | 4x2=3600 | B. | 100×50-4x2=3600 | ||
| C. | (100-x)(50-x)=3600 | D. | (100-2x)(50-2x)=3600 |
18.在密码学中,把直接可以看到的内容称为明码,对明码进行某种处理后得到的内容称为密码.有一种密码,将英文26个字母a,b,c,…z依次对应1、2、3,…,26这26个自然数,如下表,当明码对应的序号x为奇数时,密码对应的序号y=$\frac{x+1}{2}$;当明码对应的序号x为偶数时,密码对应的序号y=$\frac{x}{2}+13$.
按上述规定,将明码“love”译成密码(密码是字母)是s、h、x、c.
| 字母 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 序号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
2.下列根式中,属于最简二次根式的是( )
| A. | $\sqrt{0.5mn}$ | B. | $\sqrt{{a^2}+1}$ | C. | $\sqrt{27}$ | D. | $-\sqrt{125}$ |
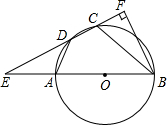 已知四边形ABCD内接于圆O,AB是直径,AD=DC,分别延长BA,CD交于点E,BF垂直EC,交EC的延长线于F.若EA=AO,BC=6,则圆O的半径4,CF的长$\frac{3\sqrt{2}}{2}$.
已知四边形ABCD内接于圆O,AB是直径,AD=DC,分别延长BA,CD交于点E,BF垂直EC,交EC的延长线于F.若EA=AO,BC=6,则圆O的半径4,CF的长$\frac{3\sqrt{2}}{2}$.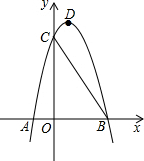 如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.
如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.