题目内容
11.已知正方形ABCD中,点E在边CD上,DE=3,EC=1.点F是正方形边上一点,且BF=AE,则FC=$\sqrt{17}$或3.分析 由正方形的性质得出BC=AB=AD=CD=DE+EC=4,∠BAD=∠C=∠D=90°,由勾股定理求出AE;分两种情况:①当点F在AD边上时,由勾股定理求出AF,得出DF,在由勾股定理求出FC即可;②当点F在CD边上时,由勾股定理求出FC即可.
解答 解: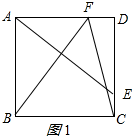 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB=AD=CD=DE+EC=4,∠BAD=∠C=∠D=90°,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
分两种情况:
①当点F在AD边上时,如图1所示:
∵BF=AE=5,
∴AF=$\sqrt{B{F}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴DF=AD-AF=1,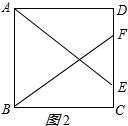
∴FC=$\sqrt{C{D}^{2}+D{F}^{2}}$=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$;
②当点F在CD边上时,如图2所示:
∵BF=AE=5,
∴FC=$\sqrt{B{F}^{2}-B{C}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3;
综上所述:FC的长为$\sqrt{17}$或3;
故答案为:$\sqrt{17}$或3.
点评 本题考查了正方形的性质、勾股定理;熟练掌握正方形的性质,由勾股定理求出AE是解决问题的突破口.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
19.下列四个实数中,绝对值最小的数是( )
| A. | -5 | B. | $-\sqrt{2}$ | C. | 1 | D. | π |
6.有一块长方形铁皮,长100cm,宽50cm,在它的四周各切去一个同样的正方形,然后将四周突出部分折起,就能制作一个无盖方盒.如果要制作的无盖方盒的底面积为3600cm2,设铁皮各角应切去的正方形边长为xcm,则下面所列方程正确的是( )
| A. | 4x2=3600 | B. | 100×50-4x2=3600 | ||
| C. | (100-x)(50-x)=3600 | D. | (100-2x)(50-2x)=3600 |
16.定义:a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数,如2的差倒数是$\frac{1}{1-2}$=-1,-1的差倒数是$\frac{1}{1-(-1)}$=$\frac{1}{2}$.已知a1=-$\frac{1}{2}$,a2是a1的差倒数,a3是a2的差倒数,a4是 a3的差倒数,…,以此类推,则a2016为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 3 | D. | 1 |
3.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.在密码学中,把直接可以看到的内容称为明码,对明码进行某种处理后得到的内容称为密码.有一种密码,将英文26个字母a,b,c,…z依次对应1、2、3,…,26这26个自然数,如下表,当明码对应的序号x为奇数时,密码对应的序号y=$\frac{x+1}{2}$;当明码对应的序号x为偶数时,密码对应的序号y=$\frac{x}{2}+13$.
按上述规定,将明码“love”译成密码(密码是字母)是s、h、x、c.
| 字母 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 字母 | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 序号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
 甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法:
甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法: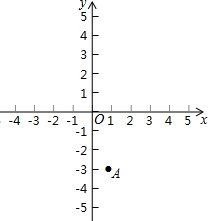 已知反比例函数y1=$\frac{k}{x}$与一次函数y2=mx+n的图象都经过A(1,-3),且当x=-3时,两个函数的函数值相等
已知反比例函数y1=$\frac{k}{x}$与一次函数y2=mx+n的图象都经过A(1,-3),且当x=-3时,两个函数的函数值相等