题目内容
1. 如图,B,C是线段AD上任意两点,M是AB的中点,N是CD中点.
如图,B,C是线段AD上任意两点,M是AB的中点,N是CD中点.(1)若MN=10cm,BC=4cm,求线段AD的长.
(2)若MN=a,BC=b,求线段AD的长.
分析 (1)首先根据M是AB的中点,N是CD中点,可得BM=AM,CN=DN,所以BM+CN=AM+DN;然后根据MN=10cm,BC=4cm,求出BM+CN的值,即可求出AM+DN的值;最后用AM+DN的值加上MN的长度,求出线段AD的长是多少即可.
(2)首先根据B,C是线段AD上任意两点,可得BM=AM,CN=DN,所以BM+CN=AM+DN;然后根据MN=acm,BC=bcm,求出BM+CN的值,即可求出AM+DN的值;最后用AM+DN的值加上MN的长度,求出线段AD的长是多少即可.
解答 解:(1)∵M是AB的中点,N是CD中点,
∴BM=AM,CN=DN,
∴BM+CN=AM+DN;
∵MN=10cm,BC=4cm,
∴BM+CN=10-4=6(cm),
∴AM+DN=6(cm),
∴AD=6+10=16(cm).
(2)∵B,C是线段AD上任意两点,
∴BM=AM,CN=DN,
∴BM+CN=AM+DN;
∵MN=acm,BC=bcm,
∴BM+CN=a-b(cm),
∴AM+DN=a-b(cm),
∴AD=a-b+a=2a-b(cm).
点评 此题主要考查了两点间的距离的求法,要熟练掌握,解答此题的关键是要明确:连接两点间的线段的长度叫两点间的距离,并能求出AM+DN的值是多少.

练习册系列答案
相关题目
16.下面四个图形中,∠1与∠2是对顶角的图形为( )
| A. | 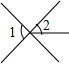 | B. | 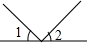 | C. | 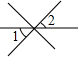 | D. | 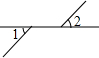 |
6.下列各组线段中,能构成直角三角形的是( )
| A. | 4cm,5cm,6cm | B. | 1cm,1cm,$\sqrt{2}$cm | C. | 6cm,8cm,11cm | D. | 5cm,12cm,23cm |
10. 如图所示的几何体是一个正三棱柱,以下不是其三视图的是( )
如图所示的几何体是一个正三棱柱,以下不是其三视图的是( )
 如图所示的几何体是一个正三棱柱,以下不是其三视图的是( )
如图所示的几何体是一个正三棱柱,以下不是其三视图的是( )| A. |  | B. |  | C. |  | D. |  |
